摘要：15．半径为1的圆的内接正三角形.正四边形.正六边形的边心距分别为多少?它们的长不能构成三角形吗?若能将构成什么形状的三角形?若不能说明理由．
网址：http://m.1010jiajiao.com/timu3_id_447416[举报]
下面说法正确的个数是 个．
①若α、β均为锐角，且α+β=90°，sinα=
，则cosβ=
；
②半径相等的圆内接正三角形、正方形、正六边形的边长之比为＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞3
：
：1；
③对角线互相平分且相等的四边形是矩形；
④关于x的一元二次方程kx2+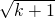
x+1=0有两个不相等的实数根，则k的取值范围是k＜且k≠0．
- A.1
- B.2
- C.3
- D.4
下面说法正确的个数是（ ）个．
①若α、β均为锐角，且α+β=90°，sinα=
，则cosβ=
；
②半径相等的圆内接正三角形、正方形、正六边形的边长之比为＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞3
：
：1；
③对角线互相平分且相等的四边形是矩形；
④关于x的一元二次方程kx2+
x+1=0有两个不相等的实数根，则k的取值范围是k＜
且k≠0．
①若α、β均为锐角，且α+β=90°，sinα=
| 1 |
| 3 |
2
| ||
| 3 |
②半径相等的圆内接正三角形、正方形、正六边形的边长之比为＜“m“：math dsi：zoomscale=150 dsi：_mathzoomed=1＞3
| 3 |
| 2 |
③对角线互相平分且相等的四边形是矩形；
④关于x的一元二次方程kx2+
| k+1 |
| 1 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
下列语句，说法正确的有
①下列各数：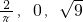
，0.2
，
，
，
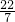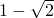中无理数有4个；
②经过平面内任意三点可作一个圆
③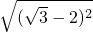
=
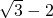
④各边相等的圆内接四边形是正方形
⑤⊙0中，半径r=1cm，弦AB、AC的长度分别为cm，1cm，则弦AB、AC所夹的角为90°．
- A.0个
- B.1个
- C.2个
- D.3个