题目内容
下列语句,说法正确的有
①下列各数: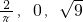 ,0.2
,0.2 ,
, ,
,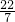 ,
,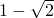 中无理数有4个;
中无理数有4个;
②经过平面内任意三点可作一个圆
③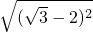 =
=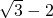
④各边相等的圆内接四边形是正方形
⑤⊙0中,半径r=1cm,弦AB、AC的长度分别为 cm,1cm,则弦AB、AC所夹的角为90°.
cm,1cm,则弦AB、AC所夹的角为90°.
- A.0个
- B.1个
- C.2个
- D.3个
B
分析:①利用无理数的概念分别分析得出即可;
②利用确定圆的条件判断得出即可;
③利用二次根式的性质化简得出即可;
④利用圆内接多边形的性质以及圆心角定理得出即可;
⑤根据当AB,AC在圆心O的同旁时或两旁时利用等边三角形的性质以及锐角三角函数关系得出即可.
解答:①下列各数: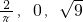 ,0.2
,0.2 ,
, ,
,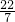 ,
,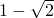 中无理数有
中无理数有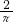 ,1-
,1- 共2个,故此选项错误;
共2个,故此选项错误;
②经过平面内不在同一直线的三点可作一个圆,故此选项错误;
③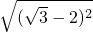 =2-
=2- ,故此选项错误;
,故此选项错误;
④各边相等的圆内接四边形是正方形,利用圆内接四边形当边相等则对应弧相等,则对应内角相等,故是正方形,此选项正确;
⑤⊙0中,半径r=1cm,弦AB、AC的长度分别为 cm,1cm,则弦AB、AC所夹的角为90°.
cm,1cm,则弦AB、AC所夹的角为90°.
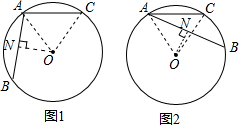
如图1,过O点作AB的垂线,垂足为N,连接OA,OC,
∵AO=CO=AC=1,
∴△AOC是等边三角形,
由垂径定理可知AN= AB=
AB= ,
,
在Rt△AOM中,cos∠OAB= ,∴∠OAB=30°,
,∴∠OAB=30°,
∴弦AB、AC所夹的角为90°,∠BAC=∠OAB+∠OAC=90°,
如图2,当AB,AC在圆心O的同旁时,
弦AB、AC所夹的角为90°,∠BAC=∠OAB-∠OAC=30°.
∴弦AB、AC所夹的角为90°或30°,故此选项错误.
故正确的有1个.
故选:B.
点评:此题主要考查了二次根式的性质以及无理数的概念和确定圆的条件以及正多边形和圆以及锐角三角函数的计算等知识,利用分类讨论得出是解题关键.
分析:①利用无理数的概念分别分析得出即可;
②利用确定圆的条件判断得出即可;
③利用二次根式的性质化简得出即可;
④利用圆内接多边形的性质以及圆心角定理得出即可;
⑤根据当AB,AC在圆心O的同旁时或两旁时利用等边三角形的性质以及锐角三角函数关系得出即可.
解答:①下列各数:
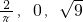 ,0.2
,0.2 ,
, ,
,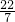 ,
,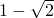 中无理数有
中无理数有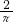 ,1-
,1- 共2个,故此选项错误;
共2个,故此选项错误;②经过平面内不在同一直线的三点可作一个圆,故此选项错误;
③
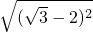 =2-
=2- ,故此选项错误;
,故此选项错误;④各边相等的圆内接四边形是正方形,利用圆内接四边形当边相等则对应弧相等,则对应内角相等,故是正方形,此选项正确;
⑤⊙0中,半径r=1cm,弦AB、AC的长度分别为
 cm,1cm,则弦AB、AC所夹的角为90°.
cm,1cm,则弦AB、AC所夹的角为90°.如图1,过O点作AB的垂线,垂足为N,连接OA,OC,
∵AO=CO=AC=1,
∴△AOC是等边三角形,
由垂径定理可知AN=
 AB=
AB= ,
,
在Rt△AOM中,cos∠OAB=
 ,∴∠OAB=30°,
,∴∠OAB=30°,∴弦AB、AC所夹的角为90°,∠BAC=∠OAB+∠OAC=90°,
如图2,当AB,AC在圆心O的同旁时,
弦AB、AC所夹的角为90°,∠BAC=∠OAB-∠OAC=30°.
∴弦AB、AC所夹的角为90°或30°,故此选项错误.
故正确的有1个.
故选:B.
点评:此题主要考查了二次根式的性质以及无理数的概念和确定圆的条件以及正多边形和圆以及锐角三角函数的计算等知识,利用分类讨论得出是解题关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目