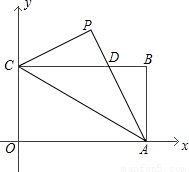
摘要:已知:如图.矩形的长.宽.将沿翻折得. (1)填空:度.点坐标为 , (2)若两点在抛物线上.求的值,并说明点在此抛物线上, 中的抛物线段(不包括点)上.是否存在一点.使得四边形 的面积最大?若存在.求出这个最大值及此时点的坐标,若不存在.请说明理由. 答案:解:(1). -- (2)点.在抛物线上. 抛物线的解析式为 -- 点坐标为 -- 点在此抛物线上. (3)假设存在这样的点.使得四边形的面积最大. 面积为定值. 要使四边形的面积最大.只需使的面积最大. 过点作轴分别交和轴于和.过点作轴交于. 设. .有最大值. 当时.的最大值是. 四边形的面积的最大值为. 此时点的坐标为. 所以存在这样的点.使得四边形的面积最大.其最大值为.-
网址:http://m.1010jiajiao.com/timu3_id_447398[举报]
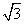 ,宽OC=1,将△AOC沿AC翻折得△APC。
,宽OC=1,将△AOC沿AC翻折得△APC。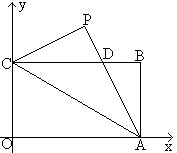
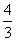 x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上; ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.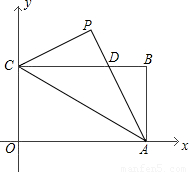
 ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.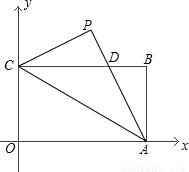
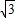 ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.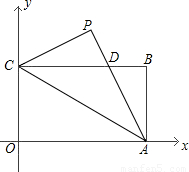
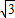 ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.