题目内容
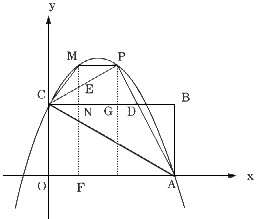
已知如图,矩形OABC的长OA=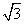 ,宽OC=1,将△AOC沿AC翻折得△APC。
,宽OC=1,将△AOC沿AC翻折得△APC。
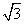 ,宽OC=1,将△AOC沿AC翻折得△APC。
,宽OC=1,将△AOC沿AC翻折得△APC。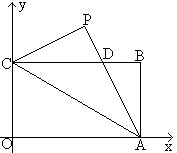
(1)填空:∠PCB=____度,P点坐标为( , );
(2)若P,A两点在抛物线y=-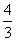 x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由。
(2)若P,A两点在抛物线y=-
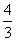 x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由。
解:(1)30,(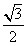 , , ); );(2)∵点P( 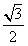 , ,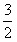 ),A( ),A(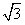 ,0)在抛物线上 ,0)在抛物线上∴ 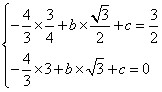 ∴ 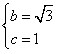 ∴抛物线的解析式为y=- 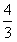 x2+ x2+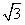 x+1 x+1C点坐标为(0,1) ∵- 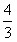 ×02+ ×02+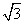 ×0+1=1 ×0+1=1 ∴C点在此抛物线上。 |
|
| (3)假设存在这样的点M,使得四边形MCAP的面积最大 ∵△ACP面积为定值, ∴要使四边形MCAP的面积最大,只需使△PCM的面积最大 过点M作MF⊥x轴分别交CP、CB和x轴于E、N和F,过点P作PG⊥x轴交CB于G 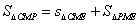 = =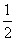 ME·CG= ME·CG=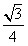 ME ME设M(x0,y0), ∵∠ECN=30°,CN=x0,∴EN= 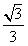 x0 x0∴ME=MF-EF=- 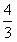 x02+ x02+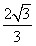 x0 x0 ∴ 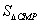 =- =-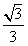 x02+ x02+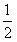 x x∵a=- 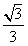 <0, <0,∴S有最大值 当x0= 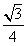 时,S的最大值是 时,S的最大值是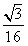 ∵ 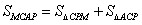 ∴四边形MCAP的面积的最大值为 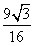 此时M点的坐标为( 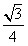 , ,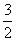 ) )所以存在这样的点M( 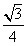 , ,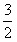 ),使得四边形MCAP的面积最大,其最大值为 ),使得四边形MCAP的面积最大,其最大值为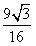 。 。 |
 |

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
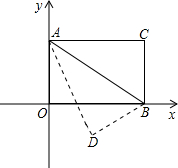 B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.


