摘要:17.已知函数的定义域为.且同时满足:①,②恒成立,③若.则有.试求: (1)的值, (2)函数的最值. (1) 在条件③中,令.得.即.················2分 又时.恒成立.. ················5分 (2)设.则必存在实数.使得. 由条件③得, . ∴. 由条件②得, . ·····························9分 故当时,有. 故函数的最小值为.最大值为. ······························12分
网址:http://m.1010jiajiao.com/timu3_id_4473417[举报]
(本题满分12分)已知函数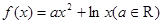
(Ⅰ)当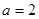 时,求
时,求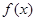 在区间
在区间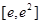 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)如果函数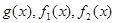 在公共定义域D上,满足
在公共定义域D上,满足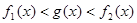 ,
,
那么就称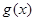 为
为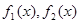 的“伴随函数”.已知函数
的“伴随函数”.已知函数
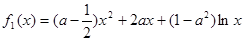 ,
,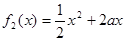 .若在区间
.若在区间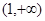 上,
上,
函数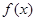 是
是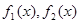 的“伴随函数”,求
的“伴随函数”,求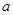 的取值范围.
的取值范围.
查看习题详情和答案>>
请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
| |||
| |||
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数![]() 的定义域为
的定义域为![]() ,
,![]() 的定义域为
的定义域为![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 空集
空集
2.已知复数![]() ,则它的共轭复数等于
,则它的共轭复数等于
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.设变量![]() 、
、![]() 满足线性约束条件
满足线性约束条件 ,则目标函数
,则目标函数![]() 的最小值为
的最小值为
![]() 6
6 ![]() 7
7 ![]() 8
8 ![]() 23
23