摘要: 如图①.矩形ABCD被对角线AC分为两个直角三角形.AB=3.BC=6.现将Rt△ADC绕点C顺时针旋转90º.点A旋转后的位置为点E,点D旋转后的位置为点F.以C为原点.以BC所在直线为轴.以过点C垂直于BC的直线为轴.建立如图②的平面直角坐标系. (1) 求直线AE的解析式, (2) 将Rt△EFC沿轴的负半轴平行移动.如图③.设OC=().Rt△EFC与Rt△ABO的重叠部分面积为s, ① 当=1与=8时,求s的值, ② S是否存在最大值?若存在.求出这个最大值及此时的值,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_447340[举报]
如图①,矩形ABCD被对角线AC分为两个直角三角形,AB=3,BC=6.现将Rt△ADC绕点C顺时针旋转90°,点A旋转后的位置为点E,点D旋转后的位置为点F.以C为原点,以BC所在直线为x轴,以过点C垂直于BC的直线为y轴,建立如图②的平面直角坐标系.

(1)求直线AE的解析式;
(2)将Rt△EFC沿x轴的负半轴平行移动,如图③.设OC=x(0<x≤9),Rt△EFC与Rt△ABO的重叠部分面积为s;求当x=1与x=8时,s的值;
(3)在(2)的条件下s是否存在最大值?若存在,求出这个最大值及此时x的值;若不存在,请说明理由.
查看习题详情和答案>>

(1)求直线AE的解析式;
(2)将Rt△EFC沿x轴的负半轴平行移动,如图③.设OC=x(0<x≤9),Rt△EFC与Rt△ABO的重叠部分面积为s;求当x=1与x=8时,s的值;
(3)在(2)的条件下s是否存在最大值?若存在,求出这个最大值及此时x的值;若不存在,请说明理由.
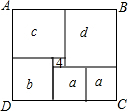 如图,矩形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,其他正方形的边长分别为a、b、c、d.求矩形ABCD中最大正方形与最小正方形的面积之差.
如图,矩形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,其他正方形的边长分别为a、b、c、d.求矩形ABCD中最大正方形与最小正方形的面积之差.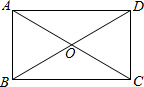 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86厘米,矩形的周长是30厘米,则对角线的长是
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86厘米,矩形的周长是30厘米,则对角线的长是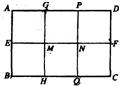 17、如图,矩形ABCD被分割成了6个边长为2的小正方形,共得到12个顶点,选取其中的三个顶点连成三角形,请回答下列问题:
17、如图,矩形ABCD被分割成了6个边长为2的小正方形,共得到12个顶点,选取其中的三个顶点连成三角形,请回答下列问题: