摘要:13.(理)设函数在区间上连续.则实数a的值为 2 . (文)在等差数列 13 .
网址:http://m.1010jiajiao.com/timu3_id_4472860[举报]
定理:若函数f(x)的图象在区间[a,b]上连续,且在(a,b)内可导,则至少存在一点ξ∈(a,b),使得f(b)-f(a)=f′(ξ)(b-a)成立.应用上述定理证明:
(1)1-
<lny-lnx<
-1(0<x<y);
(2)设bn=
,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010
(3)设f(x)=xn(n∈N*).若对任意的实数x,y,f(x)-f(y)=f′(
)(x-y)恒成立,求n所有可能的值.
查看习题详情和答案>>
(1)1-
| x |
| y |
| y |
| x |
(2)设bn=
| 1 |
| n |
(3)设f(x)=xn(n∈N*).若对任意的实数x,y,f(x)-f(y)=f′(
| x+y |
| 2 |
定理:若函数f(x)的图象在区间[a,b]上连续,且在(a,b)内可导,则至少存在一点ξ∈(a,b),使得f(b)-f(a)=f′(ξ)(b-a)成立.应用上述定理证明:
(1)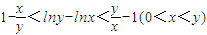 ;
;
(2)设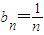 ,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010
,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010
(3)设f(x)=xn(n∈N*).若对任意的实数x,y,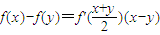 恒成立,求n所有可能的值.
恒成立,求n所有可能的值.
查看习题详情和答案>>
(1)
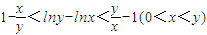 ;
; (2)设
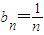 ,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010
,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010(3)设f(x)=xn(n∈N*).若对任意的实数x,y,
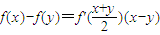 恒成立,求n所有可能的值.
恒成立,求n所有可能的值.查看习题详情和答案>>
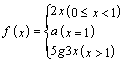 在区间
在区间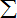
 ;
;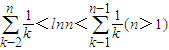 .
.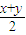 )(x-y)恒成立,求n所有可能的值.
)(x-y)恒成立,求n所有可能的值.