摘要:12.已知的一次函数.b为不等于1的常量.且设为 ( ) A.等差数列YCY B.等比数列 C.递增数列 D.递减数列
网址:http://m.1010jiajiao.com/timu3_id_4472814[举报]
已知f(x)=bx+1为x的一次函数,b为不等于1的常数,且g(n)=
,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )
|
| A、等差数列 | B、等比数列 |
| C、递增数列 | D、递减数列 |
已知二次函数f(x)=ax2+bx+c.
(1)若a>b>c,且f(1)=0,是否存在m∈R,使得f(m)=-a成立时,f(m+3)为正数,若存在,证明你的结论,若不存在,说明理由;
(2)若对x1,x2∈R,且x1<x2,f(x1)≠f(x2),方程f(x)=
[f(x1)+f(x2)]有2个不等实根,证明必有一个根属于(x1,x2).
(3)若f(0)=0,是否存在b的值使{x|f(x)=x}={x|f[f(x)]=x}成立,若存在,求出b的取值范围,若不存在,说明理由.
查看习题详情和答案>>
(1)若a>b>c,且f(1)=0,是否存在m∈R,使得f(m)=-a成立时,f(m+3)为正数,若存在,证明你的结论,若不存在,说明理由;
(2)若对x1,x2∈R,且x1<x2,f(x1)≠f(x2),方程f(x)=
| 1 | 2 |
(3)若f(0)=0,是否存在b的值使{x|f(x)=x}={x|f[f(x)]=x}成立,若存在,求出b的取值范围,若不存在,说明理由.
 f(x)=bx+1,为关于x的一次函数,b不等0且不等于1的常数,若
f(x)=bx+1,为关于x的一次函数,b不等0且不等于1的常数,若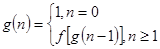 设
设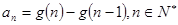 ,则数列
,则数列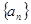 为
为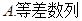
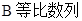
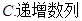
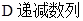
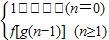 ,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )
,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )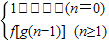 ,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )
,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )