题目内容
已知f(x)=bx+1为x的一次函数,b为不等于1的常数,且g(n)=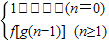 ,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )
,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )A.等差数列
B.等比数列
C.递增数列
D.递减数列
【答案】分析:根据g(n)的通项公式可求得g(1),g(2),g(3)直至g(n),进而可求a1,a2,a3,┉,an进而发现数列{an}是等比数列
解答:解:已知f(x)=bx+1为x的一次函数,b为不等于1的常数,且
g(n)=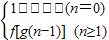 ,
,
则g(1)=b+1,g(2)=b2+b+1,g(3)=b3+b2+b+1,┉,g(n)=bn+┉+b2+b+1.
a1=b,a2=b2,a3=b3,┉,an=bn
故数列{an}是等比数列
点评:本题主要考查等比关系的确定.属基础题.
解答:解:已知f(x)=bx+1为x的一次函数,b为不等于1的常数,且
g(n)=
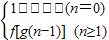 ,
,则g(1)=b+1,g(2)=b2+b+1,g(3)=b3+b2+b+1,┉,g(n)=bn+┉+b2+b+1.
a1=b,a2=b2,a3=b3,┉,an=bn
故数列{an}是等比数列
点评:本题主要考查等比关系的确定.属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)=bx+1为x的一次函数,b为不等于1的常数,且g(n)=
,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )
|
| A、等差数列 | B、等比数列 |
| C、递增数列 | D、递减数列 |
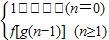 ,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )
,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( ) ,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )
,设an=g(n)-g(n-1) (n∈N*),则数列{an}是( )