摘要：3．给出下列四个命题.其中正确的命题是 ( ) A．函数在其定义域中是减函数 B．函数的最小正周期是π C．函数上是增函数 D．函数是奇函数
网址：http://m.1010jiajiao.com/timu3_id_4472805[举报]
给出下列四个命题，其中正确的命题的个数为（ ）
①命题“存在x0∈R，2x0≤0”的否定是“．对任意的x∈R，2x＞0”；
②函数y=tan
的对称中心为（kπ，0），k∈Z；
③log2sin
+log2cos
=-2；
④[cos（3-2x）]′=-2sin（3-2x）．
①命题“存在x0∈R，2x0≤0”的否定是“．对任意的x∈R，2x＞0”；
②函数y=tan
| x |
| 2 |
③log2sin
| π |
| 12 |
| π |
| 12 |
④[cos（3-2x）]′=-2sin（3-2x）．
查看习题详情和答案>>
给出下列四个命题，其中正确的命题的个数为（ ）
①命题“存在x∈R，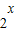
≤0”的否定是“．对任意的x∈R，2x＞0”；
②函数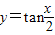
的对称中心为（kπ，0），k∈Z；
③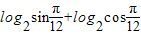
=-2；
④[cos（3-2x）]′=-2sin（3-2x）．
A．1
B．2
C．3
D．4
查看习题详情和答案>>
①命题“存在x∈R，
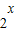≤0”的否定是“．对任意的x∈R，2x＞0”；②函数
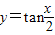的对称中心为（kπ，0），k∈Z；③
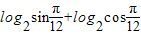=-2；④[cos（3-2x）]′=-2sin（3-2x）．
A．1
B．2
C．3
D．4
查看习题详情和答案>>
给出下列四个命题，其中正确的命题的个数为（ ）
①命题“?x∈R，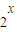
≤0”的否定是“?x∈R，2x＞0”；
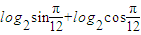②
=-2；
③函数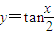
的对称中心为（kπ，0），k∈Z；
④[cos（3-2x）]′=-2sin（3-2x）
A．1
B．2
C．3
D．4
查看习题详情和答案>>
①命题“?x∈R，
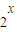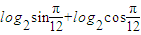≤0”的否定是“?x∈R，2x＞0”；②
=-2；③函数
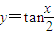的对称中心为（kπ，0），k∈Z；④[cos（3-2x）]′=-2sin（3-2x）
A．1
B．2
C．3
D．4
查看习题详情和答案>>
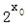≤0”的否定是“．对任意的x∈R，2x＞0”；
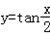的对称中心为（kπ，0），k∈Z；
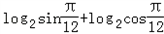=﹣2；