摘要：21．解:(1)由∣ax-1∣<x ó ó 1当0<a≦1时.x>; 2<x<;---5分 ∴当0<a≦1时.M={x∣x>}; a>1时, M={x∣<x<}--6分 =cosx-sinx=cos(x+)---7分 由2k≦x+≦2k+ ,得2k-≦x≦2k+. ∴当0<a≦1时,f(x)在M上不单调. 当a>1时. 此时.只能k=0才有解.a≧. 故a的最小值为---12分
网址：http://m.1010jiajiao.com/timu3_id_4472543[举报]
设函数f（x）=
在[1，+∞
上为增函数.
（1）求正实数a的取值范围；
（2）比较
的大小，说明理由；
（3）求证：
（n∈N*, n≥2）
【解析】第一问中，利用
解:（1）由已知：
，依题意得：
≥0对x∈[1，+∞恒成立
∴ax－1≥0对x∈[1，+∞恒成立 ∴a－1≥0即：a≥1
（2）∵a=1 ∴由（1）知：f（x）=
在[1，+∞)上为增函数，
∴n≥2时：f（
）=
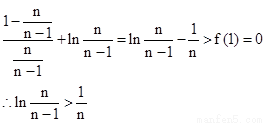
(3) ∵
∴
查看习题详情和答案>>
由2x+1＞42-x，得2x+1＞22（2-x），
解得x+1＞2（2-x），即x＞1，
所以a=2．
即方程（1-|2x-1|）=ax-1为（1-|2x-1|）=2x-1，
所以2-|2x-1|=2x，
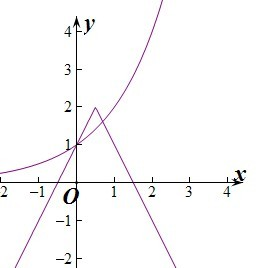
设y=2-|2x-1|，y=2x，
分别在坐标系中作出两个函数的图象，由图象可知两函数的交点个数为2个．
即方程（1-|2x-1|）=ax-1实数根的个数为2个．
故选C．