摘要：已知函数 (k为常数).A(-2k, 2)是函数图象上的点. (I)求实数k的值及函数的解析式, (II)将的图象按向量(3.0)平移.得到函数y=g(x)的图象.若恒成立.试求实数m的取值范围. 解:是函数y=f-1(x)图象上的点. ∴B上的点. ∴2k=32+k ∴k=-3, ∴y=f(x)=3x-3 ∴y=f-1(x)=log3 (II)将y=f-1(x)的图象按向量==log3x 要使2f-1(x+)-g(x)≥1 恒成立. 即使2log3(x+)-log3x≥1恒成立. 所以有x+≥3在x>0时恒成立.只须(x+)min≥3. 又x+(当且仅当x=时取等号) ∴(x+)min=4 只须4≥3.即m≥. ∴实数m的取值范围为
网址：http://m.1010jiajiao.com/timu3_id_4471884[举报]
(本小题满分12分)
已知函数f（x）=x3－ax2，其中a为实常数.
（1）设当x∈（0，1）时，函数y = f（x）图象上任一点P处的切线的斜线率为k，若k≥－1，求a的取值范围
（2）当x∈［－1，1］时，求函数y=f（x）+a（x2－3x）的最大值.
查看习题详情和答案>>
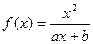（a，b为常数）且方程f(x)－x+12=0有两个实根为x1="3," x2=4.（1）求函数f(x)的解析式；（2）设k>1，解关于x的不等式；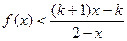
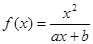（a，b为常数）且方程f(x)－x+12=0有两个实根为x1=3, x2=4.（1）求函数f(x)的解析式；（2）设k>1，解关于x的不等式；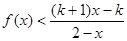
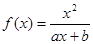（a，b为常数）且方程f(x)－x+12=0
.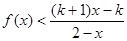