摘要:在数列中.且前n项和则的 值( ) A.2003 B.2004 C.2005 D.2006 8 直线方程Ax+By=0.若从0.1.2.4.,5.7这六个数字中每次取两个不同的数作为系数A.B的值.则方程表示不同直线的条数是 A.20 B.18 C.14 D.12 9如图已知正方体ABCD-A1B1C1D1.点M.N分别在AB1.BC1上.且AM=BN.则 ①AA1⊥MN,②A1C1∥MN,③MN∥平面A1B1C1D1,④MN与A1C1异面. 以上4个结论中.不正确的结论的个数为 4
网址:http://m.1010jiajiao.com/timu3_id_4471417[举报]
已知数列{an}中,a2=a(a为非零常数),其前n项和Sn满足:Sn=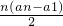 (n∈N*).
(n∈N*).
(1)求数列{an}的通项公式;
(2)若a=2,且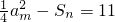 ,求m、n的值;
,求m、n的值;
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
已知数列{an}中,a2=a(a为非零常数),其前n项和Sn满足:Sn=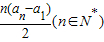
(1)求数列{an}的通项公式;
(2)若a=2,且 am2-Sn=11,求m、n的值;
am2-Sn=11,求m、n的值;
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
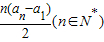
(1)求数列{an}的通项公式;
(2)若a=2,且
 am2-Sn=11,求m、n的值;
am2-Sn=11,求m、n的值;(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
已知数列{an}中,a2=a(a为非零常数),其前n项和Sn满足:Sn=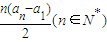
(1)求数列{an}的通项公式;
(2)若a=2,且 am2-Sn=11,求m、n的值;
am2-Sn=11,求m、n的值;
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
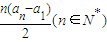
(1)求数列{an}的通项公式;
(2)若a=2,且
 am2-Sn=11,求m、n的值;
am2-Sn=11,求m、n的值;(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
查看习题详情和答案>>