题目内容
已知数列{an}中,a2=a(a为非零常数),其前n项和Sn满足:Sn=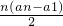 (n∈N*).
(n∈N*).
(1)求数列{an}的通项公式;
(2)若a=2,且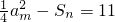 ,求m、n的值;
,求m、n的值;
(3)是否存在实数a、b,使得对任意正整数p,数列{an}中满足an+b≤p的最大项恰为第3p-2项?若存在,分别求出a与b的取值范围;若不存在,请说明理由.
解:(1)由已知,得a1=S1=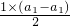 =0,∴Sn=
=0,∴Sn=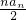 ,
,
则有Sn+1=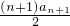 ,
,
∴2(Sn+1-Sn)=(n+1)an+1-nan,即(n-1)an+1=nan n∈N*,
∴nan+2=(n+1)an+1,
两式相减得,2an+1=an+2+an n∈N*,
即an+1-an+1=an+1-an n∈N*,
故数列{an}是等差数列.
又a1=0,a2=a,∴an=(n-1)a.
(2)若a=2,则an=2(n-1),∴Sn=n(n-1).
由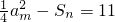 ,得n2-n+11=(m-1)2,即4(m-1)2-(2n-1)2=43,
,得n2-n+11=(m-1)2,即4(m-1)2-(2n-1)2=43,
∴(2m+2n-3)(2m-2n-1)=43.
∵43是质数,2m+2n-3>2m-2n-1,2m+2n-3>0,
∴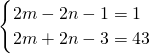 ,解得m=12,n=11.
,解得m=12,n=11.
(3)由an+b≤p,得a(n-1)+b≤p.
若a<0,则n≥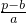 +1,不合题意,舍去;
+1,不合题意,舍去;
若a>0,则n≤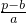 +1.∵不等式an+b≤p成立的最大正整数解为3p-2,
+1.∵不等式an+b≤p成立的最大正整数解为3p-2,
∴3p-2≤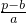 +1<3p-1,
+1<3p-1,
即2a-b<(3a-1)p≤3a-b,对任意正整数p都成立.
∴3a-1=0,解得a= ,
,
此时, -b<0≤1-b,解得
-b<0≤1-b,解得 <b≤1.
<b≤1.
故存在实数a、b满足条件,a与b的取值范围是a= ,
, <b≤1.
<b≤1.
分析:(1)利用数列的项与前n项和的关系,将条件转化为数列的项之间的关系,判定数列为特征数列,再求通项公式;
(2)利用(1)的结论,求出m、n满足的关系,分析求解即可;
(3)根据条件an+b≤p求出n满足的条件,再根据满足an+b≤p的最大项始终为3P-2,转化为不等式的恒成立问题,分析求解即可.
点评:本题考查了等差数列的通项公式,数列的项与前n项和之间的关系及数列的综合问题.
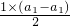 =0,∴Sn=
=0,∴Sn=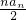 ,
,则有Sn+1=
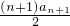 ,
,∴2(Sn+1-Sn)=(n+1)an+1-nan,即(n-1)an+1=nan n∈N*,
∴nan+2=(n+1)an+1,
两式相减得,2an+1=an+2+an n∈N*,
即an+1-an+1=an+1-an n∈N*,
故数列{an}是等差数列.
又a1=0,a2=a,∴an=(n-1)a.
(2)若a=2,则an=2(n-1),∴Sn=n(n-1).
由
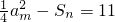 ,得n2-n+11=(m-1)2,即4(m-1)2-(2n-1)2=43,
,得n2-n+11=(m-1)2,即4(m-1)2-(2n-1)2=43,∴(2m+2n-3)(2m-2n-1)=43.
∵43是质数,2m+2n-3>2m-2n-1,2m+2n-3>0,
∴
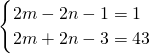 ,解得m=12,n=11.
,解得m=12,n=11.(3)由an+b≤p,得a(n-1)+b≤p.
若a<0,则n≥
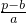 +1,不合题意,舍去;
+1,不合题意,舍去; 若a>0,则n≤
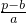 +1.∵不等式an+b≤p成立的最大正整数解为3p-2,
+1.∵不等式an+b≤p成立的最大正整数解为3p-2,∴3p-2≤
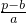 +1<3p-1,
+1<3p-1,即2a-b<(3a-1)p≤3a-b,对任意正整数p都成立.
∴3a-1=0,解得a=
 ,
,此时,
 -b<0≤1-b,解得
-b<0≤1-b,解得 <b≤1.
<b≤1.故存在实数a、b满足条件,a与b的取值范围是a=
 ,
, <b≤1.
<b≤1.分析:(1)利用数列的项与前n项和的关系,将条件转化为数列的项之间的关系,判定数列为特征数列,再求通项公式;
(2)利用(1)的结论,求出m、n满足的关系,分析求解即可;
(3)根据条件an+b≤p求出n满足的条件,再根据满足an+b≤p的最大项始终为3P-2,转化为不等式的恒成立问题,分析求解即可.
点评:本题考查了等差数列的通项公式,数列的项与前n项和之间的关系及数列的综合问题.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|