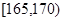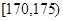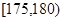摘要：4．[北 京 四 中2005年数学第一次统测] 如图.分别是正方体的棱上的点. (1)若.求证:无论点在上如何移动.总有, (2)若.且平面.求二面角的大小. 4.(I)证法一:连AC.BD.则BD⊥AC. ∵. ∴MN//AC.∴BD⊥MN. 又∵DD1⊥平面ABCD.∴DD1⊥MN. ∴MN⊥平面BDD1. ∵无论点P在DD1上如何移动.总有BP平面BDD1. 故总有MN⊥BP. 证法二:连结AC.BD.则AC⊥BD. ∵. ∴MN//AC.∴ MN⊥BD.又PD⊥平面ABCD. 由三垂线定理得:MN⊥PB. (II)解法一:过P作PG⊥C1C交CC1于G.连BG交B1N于O1. ∵PB⊥平面B1MN. ∴PB⊥B1N. 又∵PG⊥平面B1BCC1. ∴ BG⊥B1N.∴ΔBB1N≌ΔBCG. ∴ BN=CG.NC=GC1. ∴BN∶NC=DP∶PD1=2∶1. 同理BM∶MA=DP∶PD1=2∶1. 设AB=3a, 则BN=2a, ∴, , 连MO1.∵AB⊥平面B1BCC1. ∴ MO1⊥B1N. ∵∠MO1B就是二面角M-B1N-B的平面角. .∴ . 解法二:设BD与MN相交于F.连结B1F. ∵PB⊥平面MNB1. ∴ PB⊥B1F.PB⊥MN. ∴在对角面BB1D1D内.ΔPBD∽ΔBB1F. 设BB1=DD1=3.则PD=2..∴. 即.故. ∵MN⊥PB.由三垂线定理得MN⊥BD.MN//AC.MN=2BF=. BN=2. . 设二面角B-B1N-M的平面角为α.则. .
网址：http://m.1010jiajiao.com/timu3_id_4471166[举报]
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
| 组别 | 候车时间 |
|
|
| [0,5) | 2 |
| 二 | [5,10) | 6 |
| 三 | [10,15) | 4 |
| 四 | [15,20) | 2 |
| 五 | [20,25] | 1 |
(1)求这15名乘客的平
均候车时间.
(2)估计这6
0名乘客中候车时间少于10分钟的人数.
(3)若从上表第三和第四组的6人中随机抽取2人进行问卷调查,求抽到的两人恰好来自不同组的概率.
查看习题详情和答案>>、为加大西部开发步伐，国家支持西部地区选拔优秀“村官”深入农村开展工作，某市在2010年的“村官”选拔考试中随机抽取100名考生的成绩，按成绩分组，得到的频率分布表如下图所示：
（1）请先求出频率分布表中①、②位置的相应数据，再完成下面的频率分布直方图；
|
组号 |
分组 |
频数 |
频率 |
|
第一组 |
|
5 |
0.05 |
|
第二组 |
|
① |
0.35 |
|
第三组 |
|
30 |
② |
|
第四组 |
|
20 |
0.20 |
|
第五组 |
|
10 |
0.10 |
|
合计 |
100 |
1.00 |
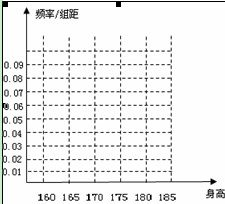
（2）为了能够选拔出最优秀的“村官”到农村一线，市委组织部决定在笔试成绩高的第三、四、五组中用分层抽样抽取6名考生进入第二轮面试，求第3，4，5组每组各抽取多少考生进入第二轮面试？
查看习题详情和答案>>
有两辆汽车由南向北驶入四叉路口，各车向左转，向右转或向前行驶的概率相等，且各车的驾驶员相互不认识．
（I）规定：“第一辆车向左转，第二辆车向右转”这一基本事件用“（左，右）”表示．又“（直，左）”表示的是基本事件：“第一辆车向前直行，第二车向左转”．请参照上面规定列出两辆汽车过路口的所有基本事件；
（II）求至少有一辆汽车向左转的概率；
（III）设有ξ辆汽车向左转，求ξ的分布列和数学期望． 查看习题详情和答案>>
（I）规定：“第一辆车向左转，第二辆车向右转”这一基本事件用“（左，右）”表示．又“（直，左）”表示的是基本事件：“第一辆车向前直行，第二车向左转”．请参照上面规定列出两辆汽车过路口的所有基本事件；
（II）求至少有一辆汽车向左转的概率；
（III）设有ξ辆汽车向左转，求ξ的分布列和数学期望． 查看习题详情和答案>>