摘要:14.如图.A.B.C为⊙0上三点.∠ACB=200, 则∠BAO的度数为 0.
网址:http://m.1010jiajiao.com/timu3_id_447104[举报]
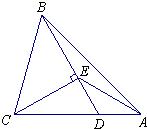 23、如图,在△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.
23、如图,在△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)求证:DE=DA;
(2)找出图中一对相似三角形,并证明.
填空并完成推理过程.
(1)如图(1),∵AB∥EF,(已知)
∴∠A+
∵DE∥BC,(已知)
∴∠DEF=
(2)如图(2),已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
解:BE∥CF,理由是:∵AB⊥BC,BC⊥CD.(已知)
∴
∵∠1=∠2,(
∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.
∴
(3)如图(3),E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
解:∵∠1=∠2,(已知)∠1=∠3,(
∴∠2=∠3,(等量代换)
∴
∴∠C=∠ABD,(
又∵∠C=∠D,(已知)
∴∠D=∠ABD,(
∴AC∥DF.(

查看习题详情和答案>>
(1)如图(1),∵AB∥EF,(已知)
∴∠A+
∠AEF
∠AEF
=180°.(两直线平行,同旁内角互补
两直线平行,同旁内角互补
)∵DE∥BC,(已知)
∴∠DEF=
∠CFE
∠CFE
,(两直线平行,内错角相等
两直线平行,内错角相等
)∠ADE=∠B
∠B
;(两直线平行,同位角相等
两直线平行,同位角相等
)(2)如图(2),已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
解:BE∥CF,理由是:∵AB⊥BC,BC⊥CD.(已知)
∴
∠ABC
∠ABC
=∠BCD
∠BCD
=90°.(垂直定义
垂直定义
)∵∠1=∠2,(
已知
已知
)∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.
∴
BE
BE
∥CF
CF
;(内错角相等,两直线平行
内错角相等,两直线平行
)(3)如图(3),E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
解:∵∠1=∠2,(已知)∠1=∠3,(
对顶角相等
对顶角相等
)∴∠2=∠3,(等量代换)
∴
BD
BD
∥CE
CE
,(同位角相等,两直线平行
同位角相等,两直线平行
)∴∠C=∠ABD,(
两直线平行,同位角相等
两直线平行,同位角相等
)又∵∠C=∠D,(已知)
∴∠D=∠ABD,(
等量代换
等量代换
)∴AC∥DF.(
内错角相等,两直线平行
内错角相等,两直线平行
)
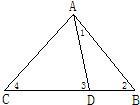 24、如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=4,∠BAC=63°,试求∠DAC,∠ADC的度数.
24、如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=4,∠BAC=63°,试求∠DAC,∠ADC的度数.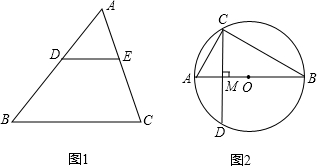 (1)如图1在△ABC中,D为AB上一点,DE∥BC交AC于点E,若AD:DB=2:3,BC=10,求DE的长.
(1)如图1在△ABC中,D为AB上一点,DE∥BC交AC于点E,若AD:DB=2:3,BC=10,求DE的长.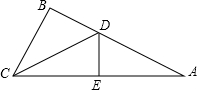 如图,在△ABC中,D为AB上的一点,连接CD,AD=CD,∠B=115°,且∠ACD:∠BCD=5:3,则∠ACB=
如图,在△ABC中,D为AB上的一点,连接CD,AD=CD,∠B=115°,且∠ACD:∠BCD=5:3,则∠ACB=