摘要:设函数.函数.其中为常数且.令函数为函数和的积函数. (1)求函数的表达式.并求其定义域, (2)当时.求函数的值域, (3)是否存在自然数.使得函数的值域恰为?若存在.试写出所有满足条件的自然数所构成的集合,若不存在.试说明理由. 解:(1).. (2)∵.∴函数的定义域为.令.则.. ∴. ∵时..又时.递减.∴单调递增. ∴.即函数的值域为. (3)假设存在这样的自然数满足条件.令.则. ∵.则.要满足值域为.则要满足. 由于当且仅当时.有中的等号成立.且此时恰为最大值. ∴. 又在上是增函数.在上是减函数.∴. 综上.得 .
网址:http://m.1010jiajiao.com/timu3_id_4471013[举报]
设函数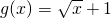 ,函数
,函数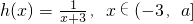 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
(1)求函数f(x)的表达式,并求其定义域;
(2)当 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(3)是否存在自然数a,使得函数f(x)的值域恰为 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
查看习题详情和答案>>
设函数 ,函数
,函数 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
(1)求函数f(x)的表达式,并求其定义域;
(2)当 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(3)是否存在自然数a,使得函数f(x)的值域恰为 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
查看习题详情和答案>>
 ,函数
,函数 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).(1)求函数f(x)的表达式,并求其定义域;
(2)当
 时,求函数f(x)的值域;
时,求函数f(x)的值域;(3)是否存在自然数a,使得函数f(x)的值域恰为
 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.查看习题详情和答案>>
设函数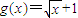 ,函数
,函数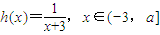 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
(1)求函数f(x)的表达式,并求其定义域;
(2)当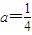 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(3)是否存在自然数a,使得函数f(x)的值域恰为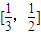 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
查看习题详情和答案>>
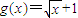 ,函数
,函数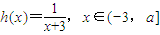 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).(1)求函数f(x)的表达式,并求其定义域;
(2)当
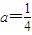 时,求函数f(x)的值域;
时,求函数f(x)的值域;(3)是否存在自然数a,使得函数f(x)的值域恰为
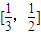 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.查看习题详情和答案>>
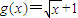 ,函数
,函数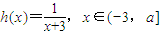 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).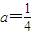 时,求函数f(x)的值域;
时,求函数f(x)的值域;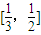 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.