题目内容
设函数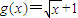 ,函数
,函数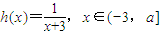 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).(1)求函数f(x)的表达式,并求其定义域;
(2)当
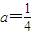 时,求函数f(x)的值域;
时,求函数f(x)的值域;(3)是否存在自然数a,使得函数f(x)的值域恰为
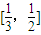 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
【答案】分析:(1)求出函数f(x)的表达式,由g(x),h(x)的定义域求解函数f(x)的定义域.
(2)当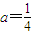 时,函数f(x)的定义域即可确定,利用换元和基本不等式求最值即可;
时,函数f(x)的定义域即可确定,利用换元和基本不等式求最值即可;
(3)结合(2)利用函数的值域求出关于a的表达式,求出a的范围即可.
解答:解:(1)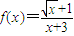 ,其定义域为[0,a];(2分)
,其定义域为[0,a];(2分)
(2)令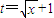 ,则
,则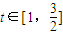 且x=(t-1)2
且x=(t-1)2
∴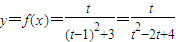 (5分)
(5分)
∴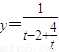
∵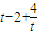 在[1,2]上递减,在[2,+∞)上递增,
在[1,2]上递减,在[2,+∞)上递增,
∴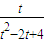 在
在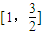 上递增,即此时f(x)的值域为
上递增,即此时f(x)的值域为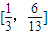 (8分)
(8分)
(3)令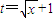 ,则
,则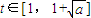 且x=(t-1)2∴
且x=(t-1)2∴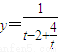
∵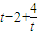 在[1,2]上递减,在[2,+∞)上递增,
在[1,2]上递减,在[2,+∞)上递增,
∴y=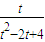 在[1,2]上递增,
在[1,2]上递增,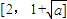 上递减,(10分)
上递减,(10分)
t=2时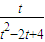 的最大值为
的最大值为 ,(11分)
,(11分)
∴a≥1,又1<t≤2时
∴由f(x)的值域恰为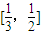 ,由
,由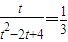 ,解得:t=1或t=4(12分)
,解得:t=1或t=4(12分)
即f(x)的值域恰为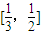 时,
时,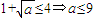 (13分)
(13分)
所求a的集合为{1,2,3,4,5,6,7,8,9}.(14分)
点评:本题考查函数的定义域,函数的值域,考查学生发现问题解决问题的能力,是中档题.
(2)当
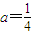 时,函数f(x)的定义域即可确定,利用换元和基本不等式求最值即可;
时,函数f(x)的定义域即可确定,利用换元和基本不等式求最值即可;(3)结合(2)利用函数的值域求出关于a的表达式,求出a的范围即可.
解答:解:(1)
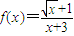 ,其定义域为[0,a];(2分)
,其定义域为[0,a];(2分)(2)令
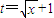 ,则
,则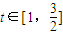 且x=(t-1)2
且x=(t-1)2∴
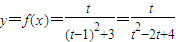 (5分)
(5分)∴
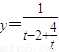
∵
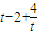 在[1,2]上递减,在[2,+∞)上递增,
在[1,2]上递减,在[2,+∞)上递增,∴
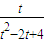 在
在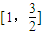 上递增,即此时f(x)的值域为
上递增,即此时f(x)的值域为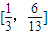 (8分)
(8分)(3)令
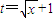 ,则
,则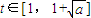 且x=(t-1)2∴
且x=(t-1)2∴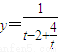
∵
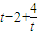 在[1,2]上递减,在[2,+∞)上递增,
在[1,2]上递减,在[2,+∞)上递增,∴y=
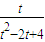 在[1,2]上递增,
在[1,2]上递增,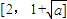 上递减,(10分)
上递减,(10分)t=2时
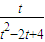 的最大值为
的最大值为 ,(11分)
,(11分)∴a≥1,又1<t≤2时

∴由f(x)的值域恰为
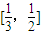 ,由
,由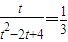 ,解得:t=1或t=4(12分)
,解得:t=1或t=4(12分)即f(x)的值域恰为
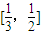 时,
时,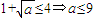 (13分)
(13分)所求a的集合为{1,2,3,4,5,6,7,8,9}.(14分)
点评:本题考查函数的定义域,函数的值域,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
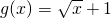 ,函数
,函数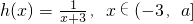 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x). 时,求函数f(x)的值域;
时,求函数f(x)的值域; ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由. ,函数
,函数 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x). 时,求函数f(x)的值域;
时,求函数f(x)的值域; ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.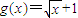 ,函数
,函数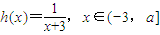 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).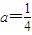 时,求函数f(x)的值域;
时,求函数f(x)的值域;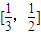 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.