摘要:已知在数列中.() (1)若.求, 若是等比数列.且是等差数列.求满足的条件, (文).若是等比数列.且是等差数列.求满足的关系式, (3)一个质点从原点出发.依次按向右.向上.向左.向下的方向交替地运动.第次运动的位移是.质点到达点.设点的横坐标为.若.求. 解:(1)∵.∴..猜测. .当=0.显然成立,当0..则, .当.显然成立,当.. (文)... (3).则.∵.∴. 由.
网址:http://m.1010jiajiao.com/timu3_id_4470991[举报]
已知在数列{an}中,a1=t,a2=t2(t>0且t≠1).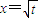 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
(1)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(2)记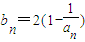 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
(3)当t=2时,是否存在指数函数g(x),使得对于任意的正整数n有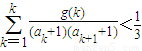 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
查看习题详情和答案>>
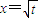 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.(1)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(2)记
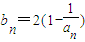 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;(3)当t=2时,是否存在指数函数g(x),使得对于任意的正整数n有
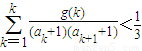 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.查看习题详情和答案>>
 中,已知
中,已知 ,
, ,且
,且 .
. ,求证:数列
,求证:数列 是等差数列;
是等差数列; , 是否总
, 是否总 使得
使得 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.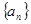 中,已知
中,已知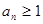 ,
,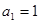 ,且
,且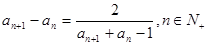 .
.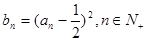 ,求证:数列
,求证:数列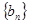 是等差数列;
是等差数列;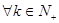 , 是否总
, 是否总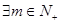 使得
使得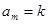 ?若存在,求出
?若存在,求出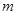 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.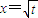 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.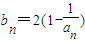 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;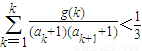 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.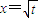 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.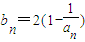 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;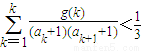 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.