摘要:已知是定义在上的函数.若对于任意的正实数.都有在上单调递增.则的图象只可能是下列图象中的( ) A B C D
网址:http://m.1010jiajiao.com/timu3_id_4470245[举报]
设函数 的定义域为
的定义域为 ,如果存在正实数
,如果存在正实数 ,对于任意
,对于任意 ,都有
,都有 ,且
,且 恒成立,则称函数
恒成立,则称函数 为
为 上的“
上的“ 型增函数”,已知函数
型增函数”,已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, ,若
,若 为
为 上的“2014型增函数”,则实数
上的“2014型增函数”,则实数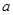 的取值范围是( )
的取值范围是( )
A. | B. | C.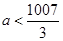 | D.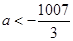 |
设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x,y,均有f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0.
(1)求 的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(2)一个各项均为正数的数列{an},它的前n项和是Sn,若a1=3,且f(Sn)=f(an)+f(an+1)-1(n≥2,n∈N*),求数列{an}的通项公式;
(3)在(2)的条件下,是否存在实数M,使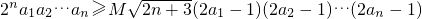 对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.
对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.
查看习题详情和答案>>
设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x,y,均有f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0.
(1)求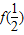 的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(2)一个各项均为正数的数列{an},它的前n项和是Sn,若a1=3,且f(Sn)=f(an)+f(an+1)-1(n≥2,n∈N*),求数列{an}的通项公式;
(3)在(2)的条件下,是否存在实数M,使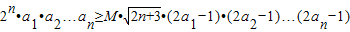 对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.
对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.
查看习题详情和答案>>
(1)求
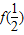 的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;(2)一个各项均为正数的数列{an},它的前n项和是Sn,若a1=3,且f(Sn)=f(an)+f(an+1)-1(n≥2,n∈N*),求数列{an}的通项公式;
(3)在(2)的条件下,是否存在实数M,使
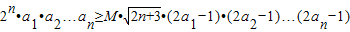 对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.
对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.查看习题详情和答案>>
设函数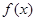 的定义域为
的定义域为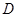 ,如果存在正实数
,如果存在正实数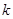 ,对于任意
,对于任意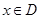 ,都有
,都有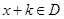 ,且
,且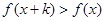 恒成立,则称函数
恒成立,则称函数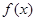 为
为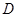 上的“
上的“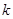 型增函数”,已知函数
型增函数”,已知函数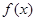 是定义在
是定义在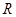 上的奇函数,且当
上的奇函数,且当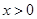 时,
时,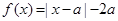 ,若
,若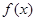 为
为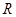 上的“2014型增函数”,则实数
上的“2014型增函数”,则实数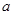 的取值范围是( )
的取值范围是( )
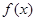 的定义域为
的定义域为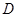 ,如果存在正实数
,如果存在正实数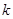 ,对于任意
,对于任意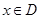 ,都有
,都有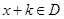 ,且
,且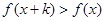 恒成立,则称函数
恒成立,则称函数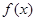 为
为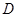 上的“
上的“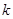 型增函数”,已知函数
型增函数”,已知函数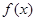 是定义在
是定义在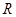 上的奇函数,且当
上的奇函数,且当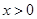 时,
时,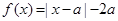 ,若
,若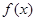 为
为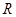 上的“2014型增函数”,则实数
上的“2014型增函数”,则实数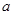 的取值范围是( )
的取值范围是( )A.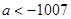 | B. | C.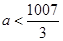 | D.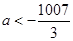 |
(1)已知函数 的定义域为
的定义域为 ,
, 是奇函数,且当
是奇函数,且当 时,
时, ,若函数
,若函数 的零点恰有两个,则实数
的零点恰有两个,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. 或 或 |
 在其定义域内任意的
在其定义域内任意的 且
且 ,有如下结论:
,有如下结论:①
 ;
;②
 ;
;③
 ;
;④
 .
.上述结论中正确结论的序号是________. 查看习题详情和答案>>