题目内容
(1)已知函数 的定义域为
的定义域为 ,
, 是奇函数,且当
是奇函数,且当 时,
时, ,若函数
,若函数 的零点恰有两个,则实数
的零点恰有两个,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. 或 或 |
 在其定义域内任意的
在其定义域内任意的 且
且 ,有如下结论:
,有如下结论:①
 ;
;②
 ;
;③
 ;
;④
 .
.上述结论中正确结论的序号是________.
(1)D;(2)②③
解析试题分析:(1)要使函数 的零点恰有两个,则根据函数是奇函数,则只需要当
的零点恰有两个,则根据函数是奇函数,则只需要当 时,函数
时,函数 的零点恰有一个即可.
的零点恰有一个即可.
(2)利用对数的基本运算性质进行检验即可.
(1)因为 是奇函数,所以
是奇函数,所以 也是奇函数,所以要使函数
也是奇函数,所以要使函数 的零点恰有两个,则只需要当
的零点恰有两个,则只需要当 时,函数
时,函数 的零点恰有一个即可.
的零点恰有一个即可.
由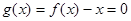 得,
得,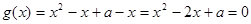 ,
,
若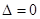 ,即
,即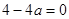 ,解得
,解得 .
.
若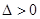 ,要使当
,要使当 时,函数
时,函数 只有一个零点,则
只有一个零点,则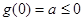 ,
,
所以此时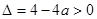 ,
, ,解得
,解得 .
.
综上 或
或 .
.
故选D.
(2)利用对数的基本运算性质进行检验:
①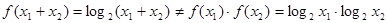 ;
;
②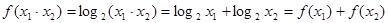 ;
;
③ 在
在 单调递增,可得
单调递增,可得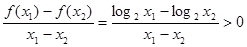 ;
;
④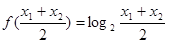 ,
,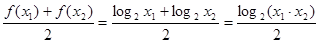 ,由基本不等式可得
,由基本不等式可得 ,从而可得
,从而可得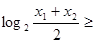
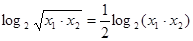 .
.
故答案为:②③.
考点:(1)函数的零点;(2)对数单调性的判断与证明;(3)基本不等式的应用.

练习册系列答案
相关题目
函数 的值域是( )
的值域是( )
A. | B. | C.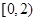 | D. |
设 则( )
则( )
A. | B. | C. | D. |
已知实数 满足
满足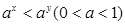 ,则下列关系式恒成立的是( )
,则下列关系式恒成立的是( )
A. | B. |
C.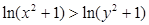 | D. |
 若
若 是
是 的最小值,则
的最小值,则 的取值范围为( ).
的取值范围为( ).
| A.[-1,2] | B.[-1,0] | C.[1,2] | D. |
某电信公司推出两种手机收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内通话时间t(分钟)与电话费s(元)的函数关系如图所示,当通话150分钟时,这两种方式电话费相差( )
| A.10元 | B.20元 | C.30元 | D. 元 元 |
[2014·湛江模拟]已知函数y=loga(2-ax)在区间[0,1]上是关于x的减函数,则a的取值范围是( )
| A.(0,1) | B.(1,2) |
| C.(0,2) | D.(2,+∞) |
 ,
, 的图象可能是下列图象中的( )
的图象可能是下列图象中的( )
 +(x-1)0 ;
+(x-1)0 ;