摘要：22．设函数f(x)的定义域为R.对于任意实数x.y.总有f.且当x＞0时.0＜f(x)＜1． 证明:当x＜0时.f(x)＞1, 在R上单调递减,·f}.N＝{y|f(ax2+x+1-y)＝1.x∈R}.且M∩N≠φ.求a的取值范围．
网址：http://m.1010jiajiao.com/timu3_id_4470133[举报]
设函数f(x)的定义域为R，对于任意实数x，y，总有f(x+y)=f(x)f(y)，且当x＞0时,0＜f(x)＜1.
(Ⅰ)求f(0)的值；
(Ⅱ)确定f(x)的单调区间；
(Ⅲ)若M={y|f(y)·f(1-a)≥f(1)}，N={y|f(ax2+x+1-y)=1，x∈R}，且M∩N≠
，求a的取值范围.·
设函数f(x)的定义域为R，对于任意的实数x、y都有f(x＋y)＝f(x)＋f(y)，又当x＞0时，f(x)＜0，且f(2)＝－1．
(1)求证：f(x)为奇函数；
(2)试问函数f(x)在区间[－6，6]上是否存在最大值与最小值？若存在，求出最大值、最小值；若不存在，请说明理由．
设函数f(x)的定义域为R，对于任意实数x，y，总有f(x＋y)＝f(x)f(y)，且当x＞0时，0＜f(x)＜1．
(Ⅰ)求f(0)的值；
(Ⅱ)确定f(x)的单调区间；
(Ⅲ)若M＝{y|f(y)·f(1－a)≥f(1)}，N＝{y|f(ax2＋x＋1－y)＝1，x∈R}，且M∩N≠
，求a的取值范围．
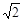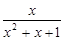(sinx+cosx)；
④f(x)=
；
(sinx+cosx)； ④f(x)=
；