摘要:若数列{an}满足N*),则称{an}为“等方比数列 . 甲:数列{an}是等方比数列,乙:数列{an}是等比数列.则 A. 甲是乙的充分条件但不是必要条件 B. 甲是乙的必要条件但不是充分条件 C. 甲是乙的充要条件 D. 甲既不是乙的充分条件也不是乙的必要条件
网址:http://m.1010jiajiao.com/timu3_id_4470079[举报]
6.若数列{an}满足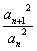 N*),则称{an}为“等方比数列”.
N*),则称{an}为“等方比数列”.
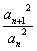 N*),则称{an}为“等方比数列”.
N*),则称{an}为“等方比数列”.甲:数列{an}是等方比数列;乙:数列{an}是等比数列.则
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
查看习题详情和答案>>
若数列{An}满足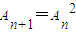 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
(Ⅰ)证明数列{2an+1}是“平方递推数列”,且数列{lg(2an+1)}为等比数列;
(Ⅱ)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项及Tn关于n的表达式;
(Ⅲ)记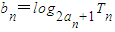 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看习题详情和答案>>
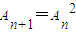 ,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.(Ⅰ)证明数列{2an+1}是“平方递推数列”,且数列{lg(2an+1)}为等比数列;
(Ⅱ)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项及Tn关于n的表达式;
(Ⅲ)记
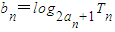 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.查看习题详情和答案>>
若数列{an}满足 N*),则称{an}为“等方比数列”甲:数列{an}是等方比数列;乙:数列{an}是等比数列.则
N*),则称{an}为“等方比数列”甲:数列{an}是等方比数列;乙:数列{an}是等比数列.则
[ ]
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
若数列{an}满足:a1=m1,a2=m2,an+2=pan+1+qan(p,q是常数),则称数列{an}为二阶线性递推数列,且定义方程x2=px+q为数列{an}的特征方程,方程的根称为特征根; 数列{an}的通项公式an均可用特征根求得:
①若方程x2=px+q有两相异实根α,β,则数列通项可以写成an=c1αn+c2βn,(其中c1,c2是待定常数);
②若方程x2=px+q有两相同实根α,则数列通项可以写成an=(c1+nc2)αn,(其中c1,c2是待定常数);
再利用a1=m1,a2=m2,可求得c1,c2,进而求得an.根据上述结论求下列问题:
(1)当a1=1,a2=2,an+2=4an+1-4an(n∈N*)时,求数列{an}的通项公式;
(2)当a1=5,a2=13,an+2=5an+1-6an(n∈N*)时,若数列{an+1-λan}为等比数列,求实数λ的值;
(3)当a1=1,a2=1,an+2=an+1+an(n∈N*)时,求Sn=a1Cn1+a2Cn2+…+anCnn的值.
查看习题详情和答案>>
①若方程x2=px+q有两相异实根α,β,则数列通项可以写成an=c1αn+c2βn,(其中c1,c2是待定常数);
②若方程x2=px+q有两相同实根α,则数列通项可以写成an=(c1+nc2)αn,(其中c1,c2是待定常数);
再利用a1=m1,a2=m2,可求得c1,c2,进而求得an.根据上述结论求下列问题:
(1)当a1=1,a2=2,an+2=4an+1-4an(n∈N*)时,求数列{an}的通项公式;
(2)当a1=5,a2=13,an+2=5an+1-6an(n∈N*)时,若数列{an+1-λan}为等比数列,求实数λ的值;
(3)当a1=1,a2=1,an+2=an+1+an(n∈N*)时,求Sn=a1Cn1+a2Cn2+…+anCnn的值.