摘要:已知函数..求: (I) 函数的最大值及取得最大值的自变量的集合, (II) 函数的单调增区间. ] 已知正方形..分别是.的中点,将沿折起,如图所示,记二面角的大小为. (I) 证明平面; (II)若为正三角形,试判断点在平面内的射影是否在直线上,证明你的结论,并求角的余弦值. 现有甲.乙两个项目.对甲项目每投资十万元.一年后利润是1.2万元.1.18万元.1.17万元的概率分别为..;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为,对乙项目每投资十万元, 取0.1.2时, 一年后相应利润是1.3万元.1.25万元.0.2万元.随机变量.分别表示对甲.乙两项目各投资十万元一年后的利润. (I) 求.的概率分布和数学期望.; (II) 当时,求的取值范围. 已知点,是抛物线上的两个动点,是坐标原点,向量,满足.设圆的方程为 (I) 证明线段是圆的直径; (II)当圆C的圆心到直线X-2Y=0的距离的最小值为时.求P的值.21. 已知函数f(x)=,其中a , b , c是以d为公差的等差数列..且a>0,d>0.设[1-]上..在.将点A. B. C (I)求 (II)若⊿ABC有一边平行于x轴.且面积为.求a ,d的值
网址:http://m.1010jiajiao.com/timu3_id_4469547[举报]
(本小题满分12分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(I)求实数a的取值范围;
(II)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设
求证: .
.
查看习题详情和答案>>
(本小题满分12分) 已知函数![]() ,
,![]() 为实数)有极值,且在
为实数)有极值,且在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(I)求实数a的取值范围;
(II)是否存在实数a,使得函数![]() 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设![]()
求证:![]() .
.
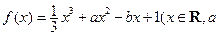 ,
,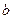 为实数)有极值,且在
为实数)有极值,且在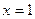 处的切线与直线
处的切线与直线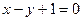 平行.
平行. (II)是否存在实数a,使得函数
(II)是否存在实数a,使得函数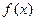 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存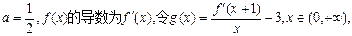
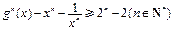 .
.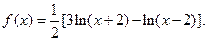
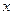 为何值时,
为何值时,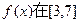 上取得最大值;
上取得最大值;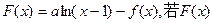 是单调递增函数,求
是单调递增函数,求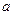 的取值范围.
的取值范围.