摘要:已知函数..求: (I) 函数的最大值及取得最大值的自变量的集合, (II) 函数的单调增区间. [解析](I) 解法一: 当,即时, 取得最大值. 函数的取得最大值的自变量的集合为. 解法二: 当,即时, 取得最大值. 函数的取得最大值的自变量的集合为. (II)解: 由题意得: 即: 因此函数的单调增区间为. [点评]本小题考查三角公式,三角函数的性质及已知三角函数值求角等基础知识,考查综合运用三角有关知识的能力. ] 已知正方形..分别是.的中点,将沿折起,如图所示,记二面角的大小为. (I) 证明平面; (II)若为正三角形,试判断点在平面内的射影是否在直线上,证明你的结论,并求角的余弦值. [解析](I)证明:EF分别为正方形ABCD得边AB.CD的中点, EB//FD,且EB=FD, 四边形EBFD为平行四边形. BF//ED 平面. (II)解法1: 如右图,点A在平面BCDE内的射影G在直线EF上, 过点A作AG垂直于平面BCDE,垂足为G,连结GC,GD. ACD为正三角形, AC=AD CG=GD G在CD的垂直平分线上, 点A在平面BCDE内的射影G在直线EF上, 过G作GH垂直于ED于H,连结AH,则,所以为二面角A-DE-C的平面角.即 设原正方体的边长为2a,连结AF 在折后图的AEF中,AF=,EF=2AE=2a, 即AEF为直角三角形, 在RtADE中, . 解法2:点A在平面BCDE内的射影G在直线EF上 连结AF,在平面AEF内过点作,垂足为. ACD为正三角形,F为CD的中点, 又因, 所以 又且 为A在平面BCDE内的射影G. 即点A在平面BCDE内的射影在直线EF上 过G作GH垂直于ED于H,连结AH,则,所以为二面角A-DE-C的平面角.即 设原正方体的边长为2a,连结AF 在折后图的AEF中,AF=,EF=2AE=2a, 即AEF为直角三角形, 在RtADE中, . 解法3: 点A在平面BCDE内的射影G在直线EF上 连结AF,在平面AEF内过点作,垂足为. ACD为正三角形,F为CD的中点, 又因, 所以 又 为A在平面BCDE内的射影G. 即点A在平面BCDE内的射影在直线EF上 过G作GH垂直于ED于H,连结AH,则,所以为二面角A-DE-C的平面角.即 设原正方体的边长为2a,连结AF 在折后图的AEF中,AF=,EF=2AE=2a, 即AEF为直角三角形, 在RtADE中, , . [点评]本小题考查空间中的线面关系,解三角形等基础知识考查空间想象能力和思维能力. 现有甲.乙两个项目.对甲项目每投资十万元.一年后利润是1.2万元.1.18万元.1.17万元的概率分别为..;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为,对乙项目每投资十万元, 取0.1.2时, 一年后相应利润是1.3万元.1.25万元.0.2万元.随机变量.分别表示对甲.乙两项目各投资十万元一年后的利润. (I) 求.的概率分布和数学期望.; (II) 当时,求的取值范围. [解析] (I)解法1: 的概率分布为 1.2 1.18 1.17 P E=1.2+1.18+1.17=1.18. 由题设得,则的概率分布为 0 1 2 P 故的概率分布为 1.3 1.25 0.2 P 所以的数学期望为 E=++=. 解法2: 的概率分布为 1.2 1.18 1.17 P E=1.2+1.18+1.17=1.18. 设表示事件 第i次调整,价格下降 ,则 P(=0)= ; P(=1)=; P(=2)= 故的概率分布为 1.3 1.25 0.2 P 所以的数学期望为 E=++=. (II) 由,得: 因0<p<1,所以时,p的取值范围是0<p<0.3. [点评]本小题考查二项分布.分布列.数学期望.方差等基础知识,考查同学们运用概率知识解决实际问题的能力. 已知点,是抛物线上的两个动点,是坐标原点,向量,满足.设圆的方程为 (I) 证明线段是圆的直径; (II)当圆C的圆心到直线X-2Y=0的距离的最小值为时.求p的值. [解析](I)证明1: 整理得: 设M(x,y)是以线段AB为直径的圆上的任意一点,则 即 整理得: 故线段是圆的直径 证明2: 整理得: --..(1) 设(x,y)是以线段AB为直径的圆上则 即 去分母得: 点满足上方程,展开并将(1)代入得: 故线段是圆的直径 证明3: 整理得: --(1) 以线段AB为直径的圆的方程为 展开并将(1)代入得: 故线段是圆的直径 (II)解法1:设圆C的圆心为C(x,y),则 又因 所以圆心的轨迹方程为 设圆心C到直线x-2y=0的距离为d,则 当y=p时,d有最小值,由题设得 . 解法2: 设圆C的圆心为C(x,y),则 又因 所以圆心的轨迹方程为 设直线x-2y+m=0到直线x-2y=0的距离为,则 因为x-2y+2=0与无公共点, 所以当x-2y-2=0与仅有一个公共点时,该点到直线x-2y=0的距离最小值为 将得 解法3: 设圆C的圆心为C(x,y),则 圆心C到直线x-2y=0的距离为d,则 又因 当时,d有最小值,由题设得 . [点评]本小题考查了平面向量的基本运算,圆与抛物线的方程.点到直线的距离公式等基础知识,以及综合运用解析几何知识解决问题的能力.21. 已知函数f(x)=,其中a , b , c是以d为公差的等差数列..且a>0,d>0.设[1-]上..在.将点A. B. C (I)求 (II)若⊿ABC有一边平行于x轴.且面积为.求a ,d的值 [解析](I)解: 令,得 当时, ; 当时, 所以f(x)在x=-1处取得最小值即 (II) 的图像的开口向上,对称轴方程为 由知 在上的最大值为 即 又由 当时, 取得最小值为 由三角形ABC有一条边平行于x轴知AC平行于x轴,所以 又由三角形ABC的面积为得 利用b=a+d,c=a+2d,得 联立可得. 解法2: 又c>0知在上的最大值为 即: 又由 当时, 取得最小值为 由三角形ABC有一条边平行于x轴知AC平行于x轴,所以 又由三角形ABC的面积为得 利用b=a+d,c=a+2d,得 联立可得 [点评]本小题考查了函数的导数,函数的极值的判定,闭区间上二次函数的最值,等差数基础知识的综合应用,考查了应用数形结合的数学思想分析问题解决问题的能力
网址:http://m.1010jiajiao.com/timu3_id_4469543[举报]
(本小题满分12分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(I)求实数a的取值范围;
(II)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设
求证: .
.
查看习题详情和答案>>
(本小题满分12分) 已知函数![]() ,
,![]() 为实数)有极值,且在
为实数)有极值,且在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(I)求实数a的取值范围;
(II)是否存在实数a,使得函数![]() 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设![]()
求证:![]() .
.
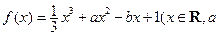 ,
,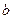 为实数)有极值,且在
为实数)有极值,且在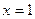 处的切线与直线
处的切线与直线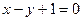 平行.
平行. (II)是否存在实数a,使得函数
(II)是否存在实数a,使得函数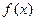 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存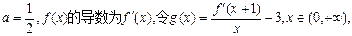
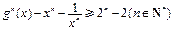 .
.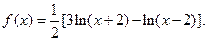
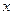 为何值时,
为何值时,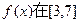 上取得最大值;
上取得最大值;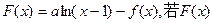 是单调递增函数,求
是单调递增函数,求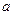 的取值范围.
的取值范围.