摘要:如图1.已知中...过点作.且.连接交于点. (1)求的长, (2)以点为圆心.为半径作⊙A.试判断与⊙A是否相切.并说明理由, (3)如图2.过点作.垂足为.以点为圆心.为半径作⊙A,以点为圆心.为半径作⊙C.若和的大小是可变化的.并且在变化过程中保持⊙A和⊙C相切.且使点在⊙A的内部.点在⊙A的外部.求和的变化范围. (1)在中.. . .. . .. (2)与⊙A相切. 在中... .. 又.. 与⊙A相切. (3)因为.所以的变化范围为. 当⊙A与⊙C外切时..所以的变化范围为, 当⊙A与⊙C内切时..所以的变化范围为.
网址:http://m.1010jiajiao.com/timu3_id_446929[举报]
如图1,已知![]() 中,
中,![]() ,
,![]() .过点
.过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() 的长;
的长;
(2)以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,试判断
,试判断![]() 与
与![]() 是否相切,并说明理由;
是否相切,并说明理由;
(3)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() .以点
.以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ;以点
;以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() .若
.若![]() 和
和![]() 的大小是可变化的,并且在变化过程中保持
的大小是可变化的,并且在变化过程中保持![]() 和
和![]() 相切,且使
相切,且使![]() 点在
点在![]() 的内部,
的内部,![]() 点在
点在![]() 的外部,求
的外部,求![]() 和
和![]() 的变化范围.
的变化范围.
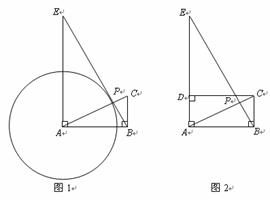
如图1,已知反比例函数y=
过点P,P点的坐标为(3-m,2m),m是分式方程
+1=
的解,PA⊥x轴于点A,PB⊥y轴于点B.
(1)求m值.
(2)试判断四边形PAOB的形状,并说明理由.
(2)如图2,连接AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连接OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
 查看习题详情和答案>>
查看习题详情和答案>>
| k |
| x |
| m-3 |
| m-2 |
| 3 |
| 2-m |
(1)求m值.
(2)试判断四边形PAOB的形状,并说明理由.
(2)如图2,连接AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连接OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
 查看习题详情和答案>>
查看习题详情和答案>>
(本题满分8分)如图1,已知反比例函数y= 过点P, P点的坐标为(3-m,
过点P, P点的坐标为(3-m,
2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.

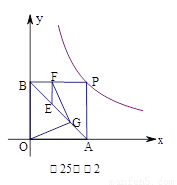
(1)求m值
(2)试判断四边形PAOB的形状,并说明理由.
(2)如图2,连结AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连结OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
查看习题详情和答案>>
 过点P, P点的坐标为(3-m,
过点P, P点的坐标为(3-m, 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.
