题目内容
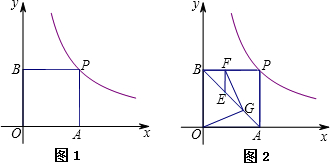
如图1,已知反比例函数y=| k |
| x |
| m-3 |
| m-2 |
| 3 |
| 2-m |
(1)求m值.
(2)试判断四边形PAOB的形状,并说明理由.
(2)如图2,连接AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连接OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
分析:(1)解出分式方程,即可求出m的值;
(2)先根据三个角都是直角判断出四边形PAOB是矩形,再根据P点坐标为(2,2)判断出PB=PA,从而判断出四边形PAOB是正方形;
(3)延长FE交OA于点H,连接GH 根据∠HFB=∠FBO=∠BOH=90°判断出BOHF是矩形,再证出△GEF≌△GHO,即可判断OG=FG.
(2)先根据三个角都是直角判断出四边形PAOB是矩形,再根据P点坐标为(2,2)判断出PB=PA,从而判断出四边形PAOB是正方形;
(3)延长FE交OA于点H,连接GH 根据∠HFB=∠FBO=∠BOH=90°判断出BOHF是矩形,再证出△GEF≌△GHO,即可判断OG=FG.
解答:解:(1)由题意解分式方程
+1=
,
整理得:
m-3+m-2=-3,
解得:m=1,
经检验知m=1是原分式方程的解.
(2)四边形PAOB是正方形.理由如下:
∵∠AOB=∠OBP=∠OAP=90°,
∴四边形PAOB是矩形,
又∵m=1,
∴P(2,2),
∴PB=PA=2,
∴四边形PAOB是正方形.
(3)OG=FG.
证明,如右图所示:
延长FE交OA于点H,连接GH,
∵∠HFB=∠FBO=∠BOH=90°,
∴BOHF是矩形,
∴BF=OH,
∵∠FBE=∠FEB=45°,
∴EF=BF=OH,
∵∠EHA=90°,G为AE的中点,
∴GH=GE=GA,
∴∠GEH=∠GAH=45°,
∴∠GEF=∠GHO,
∴△GEF≌△GHO,
∴OG=FG.
| m-3 |
| m-2 |
| 3 |
| 2-m |
整理得:
m-3+m-2=-3,
解得:m=1,
经检验知m=1是原分式方程的解.
(2)四边形PAOB是正方形.理由如下:
∵∠AOB=∠OBP=∠OAP=90°,
∴四边形PAOB是矩形,
又∵m=1,
∴P(2,2),
∴PB=PA=2,
∴四边形PAOB是正方形.
(3)OG=FG.
证明,如右图所示:

延长FE交OA于点H,连接GH,
∵∠HFB=∠FBO=∠BOH=90°,
∴BOHF是矩形,
∴BF=OH,
∵∠FBE=∠FEB=45°,
∴EF=BF=OH,
∵∠EHA=90°,G为AE的中点,
∴GH=GE=GA,
∴∠GEH=∠GAH=45°,
∴∠GEF=∠GHO,
∴△GEF≌△GHO,
∴OG=FG.
点评:本题考查了反比例函数的性质、函数图象和点的坐标特征及分式方程的解法,综合性较强,是一道难度较大的中考题,要仔细解答.

练习册系列答案
相关题目
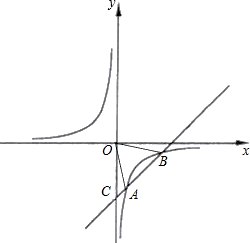 与点C(0,-4),且与反比例函数的图象相交于另一点B(3,n).
与点C(0,-4),且与反比例函数的图象相交于另一点B(3,n). (2010•皇姑区二模)如图,已知反比例函数y=
(2010•皇姑区二模)如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 点A在y轴的正半轴上,过点A作直线
点A在y轴的正半轴上,过点A作直线 ,AC:AB=2:3,则k1=( ),k2=( )。
,AC:AB=2:3,则k1=( ),k2=( )。