摘要:已知抛物线的焦点为F.A是抛物线上横坐标为4.且位于轴上方的点.A到抛物线准线的距离等于5.过A作AB垂直于轴.垂足为B.OB的中点为M. (1)求抛物线方程, (2)过M作.垂足为N.求点N的坐标, (3)以M为圆心.MB为半径作圆M.当是轴上一动点时.讨论直线AK与圆M的位置关系. [思路点拨]本题考查直线与抛物线.直线与圆的位置关系等基础知识.考查运用解析几何的方法分析问和解决问题的能力.第问是定量分析.难度不大.而解决(3)的常规方法之一就是利用点M到直线AK的距离d与圆的半径比较为宜. [正确解答] (1) 抛物线y2=2px的准线为x=-,于是4+=5, ∴p=2. ∴抛物线方程为y2=4x. , 由题意得B, 又∵F(1,0), ∴kFA=;MN⊥FA, ∴kMN=-, 则FA的方程为y=(x-1),MN的方程为y-2=-x,解方程组得x=,y=, ∴N的坐标(,). (1) 由题意得, ,圆M.的圆心是点(0,2), 半径为2, 当m=4时, 直线AK的方程为x=4,此时,直线AK与圆M相离. 当m≠4时, 直线AK的方程为y=y-4m=0, 圆心M(0,2)到直线AK的距离d=,令d>2,解得m>1 ∴当m>1时, AK与圆M相离; 当m=1时, AK与圆M相切; 当m<1时, AK与圆M相交. [解后反思]解答圆锥这部分试题需准确地把握数与形的语言转换能力.推理能力.本题计算量并不大.但步步等价转换的意识要准确无误.
网址:http://m.1010jiajiao.com/timu3_id_4469249[举报]
(本小题满分16分)
已知抛物线![]()
![]() 的准线为
的准线为![]() ,焦点为
,焦点为![]() .⊙M的圆心在
.⊙M的圆心在![]() 轴的正半轴上,且与
轴的正半轴上,且与![]() 轴相切.
轴相切.
过原点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,交
,交![]() 于点
于点![]() , 交⊙M于另一点
, 交⊙M于另一点![]() ,且
,且![]() .
.
 (Ⅰ)求⊙M和抛物线
(Ⅰ)求⊙M和抛物线![]() 的方程;
的方程;
(Ⅱ)若![]() 为抛物线
为抛物线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(Ⅲ)过![]() 上的动点
上的动点![]() 向⊙M作切线,切点为
向⊙M作切线,切点为![]() ,
,
求证:直线![]() 恒过一个定点,并求该定点的坐标.
恒过一个定点,并求该定点的坐标.
 的焦点为
的焦点为 ,
, 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于 轴上方的点.
轴上方的点.  垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为 (
( 为坐标原点).
为坐标原点).  的方程;
的方程; ,垂足为
,垂足为 ,求点
,求点 是
是 与圆
与圆
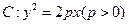 的焦点为
的焦点为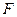 ,
,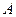 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于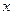 轴上方的点.
轴上方的点. 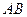 垂直于
垂直于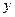 轴,垂足为
轴,垂足为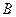 ,
,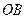 的中点为
的中点为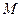 (
(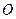 为坐标原点).
为坐标原点).
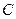 的方程;
的方程;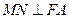 ,垂足为
,垂足为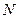 ,求点
,求点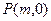 是
是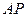 与圆
与圆