网址:http://m.1010jiajiao.com/timu3_id_4468923[举报]
(本小题满分12分)在每年的春节后,某市政府都会发动公务员参与到植树绿化活动中去.林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
甲:37,21,31, 20, 29, 19, 32, 23, 25, 33;
乙:10, 30, 47, 27, 46, 14, 26, 10, 44, 46.
(1)画出两组数据的茎叶图,并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为![]() ,将这10株树苗的高度依次输入,按程序框(如右图)进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入,按程序框(如右图)进行运算,问输出的S大小为多少?并说明S的统计学意义.

(本题满分14分)惠州市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
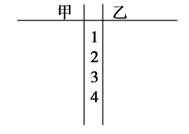
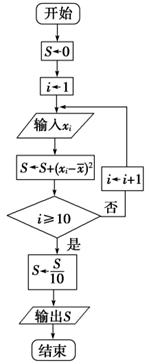
(2)设抽测的10株甲种树苗高度平均值为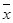 ,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.
查看习题详情和答案>>
(本题满分14分)惠州市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;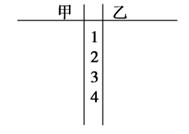
(2)设抽测的10株甲种树苗高度平均值为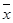 ,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.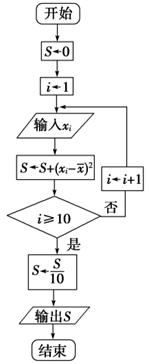
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;

(2)设抽测的10株甲种树苗高度平均值为
 ,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.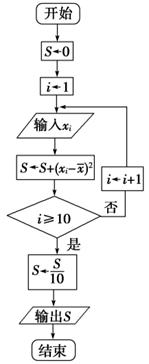
 ,求
,求