摘要:22. 当n=2时..不等式成立. (2)假设当时不等式成立.即 那么. 这就是说.当时不等式成立. 根据可知:成立. (Ⅱ)证法一: 由递推公式及(Ⅰ)的结论有 两边取对数并利用已知不等式得 故 上式从1到求和可得 即 (Ⅱ)证法二: 由数学归纳法易证成立.故 令 取对数并利用已知不等式得 上式从2到n求和得 因 故成立.
网址:http://m.1010jiajiao.com/timu3_id_4468724[举报]
(本小题满分12分)
定义在R上的函数 满足:对任意实数m,n,总有
满足:对任意实数m,n,总有 ,且当
,且当 时,
时, .
.
(1)试求 的值;
的值;
(2)判断 的单调性并证明你的结论;
的单调性并证明你的结论;
(3)若不等式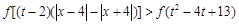 对
对 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
查看习题详情和答案>>
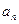 }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的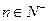 ,点
,点 ,均在函数
,均在函数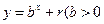 且
且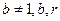 均为常数)的图像上。
均为常数)的图像上。 ,证明:对任意的
,证明:对任意的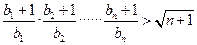 成立。
成立。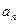 }的前n项和为
}的前n项和为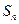 ,已知对任意的
,已知对任意的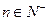 ,点
,点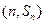 ,均在函数
,均在函数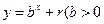 且
且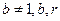 均为常数)的图像上。
均为常数)的图像上。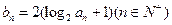 ,证明:对任意的
,证明:对任意的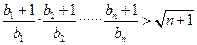 成立。
成立。