题目内容
已知函数f(x)=x2-(m+1)x+m(m为常数).
(I)若tanA,tanB是关于x的方程f(x)=0的两个根,其中A、B的锐角三角形的两个内角,求m的取值范围;
(II)当![]() 时,
时,![]() 有最小值-2,求m的值.
有最小值-2,求m的值.
答案:
解析:
解析:
答案:解:(I)由f(x)=0得,x2-(m+1)x+m=0,依题意得
综上所述,m的取值范围是m>1. (II)当x≥0时, ①当 ∴f(0)=m最小,此时m=-2;②当 ∴m2-2m-7=0,∴ .
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
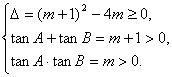 ∴m>0.又∵A、B是锐角三角形的两个内角,
∴m>0.又∵A、B是锐角三角形的两个内角,