摘要：7．在等比数列{an}中.记Sn＝a1+a2+a3+--+an.已知a5＝2S4+3, a6＝2S5+3.则此数列的公比q的值是 .
网址：http://m.1010jiajiao.com/timu3_id_4468527[举报]
等比数列{an}中，a1，a2，a3分别是下表第一、二、三行中的某一个数，且a1，a2，a3中的任何两个数不在下表的同一列．
(1)试确定a1，a2，a3的值，并求数列{an}的通项公式．
(2)若数列{bn}满足bn＝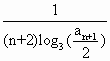
，记数列{bn}的前n项和为Sn，证明：Sn＜
．
等差数列{an}中a3＝7，a1＋a2＋a3＝12，记Sn为{an}的前n项和，令bn＝anan+1，数列{
}的前n项和为Tn．
(1)求an和Sn；
(2)求证：Tn＜
；
(3)是否存在正整数m，n，且1＜m＜n，使得T1，Tm，Tn成等比数列？若存在，求出m，n的值，若不存在，说明理由．
已知等差数列{an}的首项为a，公差为b；等比数列{bn}的首项为b，公比为a，其中a，
，且a1＜b1＜a2＜b2＜a3．
(1)求a的值；
(2)若对于任意
，总存在
，使am＋3＝bn，求b的值；
(3)在(2)中，记{cn}是所有{an}中满足am＋3＝bn，的项从小到大依次组成的数列，又记Sn为{cn}的前n项和，Tn{an}的前n项和，求证：Sn≥Tn
．
| |||||||||||||||
的首项为a，公差为b；等比数列
的首项为b，公比为a，其中a，b∈N+，且a1＜b1＜a2＜b2＜a3．
≥
(n∈N+)．
)，令bn＝an·sn，数列
的前n项和为Tn．
；