摘要:11.已知向量.则向量的坐标是 .将向量按逆时针方向旋转90°得到向量.则向量的坐标是 .
网址:http://m.1010jiajiao.com/timu3_id_4468113[举报]
已知向量 ,动点M到定直线
,动点M到定直线 的距离等于
的距离等于 ,并且满足
,并且满足 ,其中
,其中 为坐标原点,
为坐标原点, 为非负实数.
为非负实数.
(I)求动点M的轨迹方程 ;
;
(II)若将曲线 向左平移一个单位,得曲线
向左平移一个单位,得曲线 ,试判断曲线
,试判断曲线 为何种类型;
为何种类型;
(III)若(II)中曲线 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足 ,当
,当 是曲线
是曲线 的两个焦点时,则曲线
的两个焦点时,则曲线 上恒存在点P,使得
上恒存在点P,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看习题详情和答案>>
对于下列四个命题
①若向量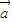 ,
,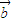 ,满足
,满足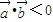 ,则
,则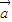 与
与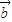 的夹角为钝角;
的夹角为钝角;
②已知集合A=正四棱柱,B=长方体,则A∩B=B;
③在直角坐标平面内,点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧;
④对2×2数表定义平方运算如下: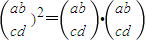 =
=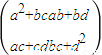 ,则
,则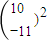 =
=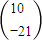
其中真命题是 (将你认为的正确命题的序号都填上). 查看习题详情和答案>>
①若向量
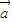 ,
,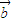 ,满足
,满足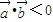 ,则
,则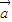 与
与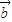 的夹角为钝角;
的夹角为钝角;②已知集合A=正四棱柱,B=长方体,则A∩B=B;
③在直角坐标平面内,点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧;
④对2×2数表定义平方运算如下:
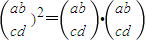 =
=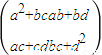 ,则
,则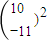 =
=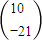
其中真命题是 (将你认为的正确命题的序号都填上). 查看习题详情和答案>>
对于下列四个命题
①若向量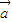 ,
,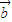 ,满足
,满足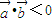 ,则
,则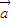 与
与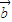 的夹角为钝角;
的夹角为钝角;
②已知集合A=正四棱柱,B=长方体,则A∩B=B;
③在直角坐标平面内,点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧;
④对2×2数表定义平方运算如下: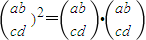 =
=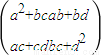 ,则
,则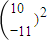 =
=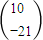
其中真命题是 (将你认为的正确命题的序号都填上). 查看习题详情和答案>>
①若向量
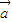 ,
,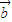 ,满足
,满足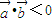 ,则
,则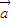 与
与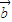 的夹角为钝角;
的夹角为钝角;②已知集合A=正四棱柱,B=长方体,则A∩B=B;
③在直角坐标平面内,点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧;
④对2×2数表定义平方运算如下:
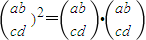 =
=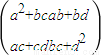 ,则
,则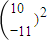 =
=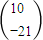
其中真命题是 (将你认为的正确命题的序号都填上). 查看习题详情和答案>>
对于下列四个命题
①若向量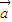 ,
,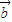 ,满足
,满足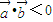 ,则
,则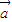 与
与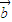 的夹角为钝角;
的夹角为钝角;
②已知集合A=正四棱柱,B=长方体,则A∩B=B;
③在直角坐标平面内,点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧;
④对2×2数表定义平方运算如下: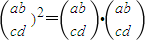 =
=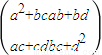 ,则
,则 =
=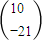
其中真命题是 (将你认为的正确命题的序号都填上). 查看习题详情和答案>>
①若向量
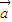 ,
,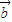 ,满足
,满足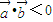 ,则
,则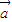 与
与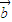 的夹角为钝角;
的夹角为钝角;②已知集合A=正四棱柱,B=长方体,则A∩B=B;
③在直角坐标平面内,点M(|a|,|a-3|)与N(cosα,sinα)在直线x+y-2=0的异侧;
④对2×2数表定义平方运算如下:
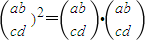 =
=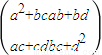 ,则
,则 =
=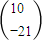
其中真命题是 (将你认为的正确命题的序号都填上). 查看习题详情和答案>>
 已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,
已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,| 3 |
| 2 |
(1)若已知下列所给的三个方程中有一个是等轴双曲线C的方程:①x2-y2=
| 27 |
| 4 |
| 9 |
| 2 |
(2)现要在等轴双曲线C上选一处P建一座码头,向A(3,3)、B(9,6)两地转运货物.经测算,从P到A、从P到B修建公路的费用都是每单位长度a万元,则码头应建在何处,才能使修建两条公路的总费用最低?
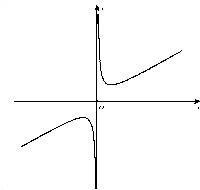
(3)如图,函数y=
| ||
| 3 |
| 1 |
| x |