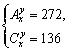摘要:(17)[解]∵ ∴ -- 于是∠C=60°.或∠C=120°. -- 又 当 ∠C=60°时. -- 当 ∠C=120°时. -- (18) [解法一]由已知 -- 根据直角的不同位置.分两种情况: 若∠PF2F1为直角.则 即 得 故 -- 若∠F1PF2为直角.则 即 得 故 -- [解法二] 由椭圆的对称性不妨设P(x.y) (x>0.y>0). 则由已知可得 -- 根据直角的不同位置.分两种情况: 若∠PF2F1为直角.则 于是故 -- 若∠F1PF2为直角.则. 解得即 于是故 -- (说明:两种情况.缺少一种扣3分) [证明]如图.以O为原点建立空间直角坐标系. 设AE=BF=x.则 A’(a.0.a).F(a-x.a.0).C’(0.a.a).E(a.x.0) -- ∵ ∴ A’F⊥C’E. (2)[解]记BF=x.BE=y.则 x+y=a. 三棱锥B’-BEF的体积 当且仅当时.等号成立. 因此.三棱锥B’-BEF的体积取得最大值时. -- 过B作BD⊥EF交EF于D.连B’D.可知B’D⊥EF. ∴ ∠B’DB是二面角B’-EF-B的平面角. 在直角三角形BEF中.直角边是斜边上的高. ∴ 故二面角B’-EF-B的大小为 -- ∵ z是方程的根. ∴ z1=i 或 z2=-i. -- 不论 z1=i 或 z2=-i. -- 于是 -- (2)取.则及 于是 或取(说明:只需写出一个正确答案.) f(0)=1表示没有用水洗时.蔬菜上的农药量将保持原样. -- (2)函数f(x)应该满足的条件和具有的性质是: 在[0,+∞]上f(x)单调递减.且0<f(x)≤1. -- (3)设仅清洗一次.残留的农药量为 清洗两次后.残留的农药量为 -- 则 于是.当时.f1>f2; 当时.f1=f2; 当时.f1<f2; 当时.清洗两次后残留的农药量较少, 当时.两种清洗方法具有相同的效果, 当时.一次清洗残留的农药量较少. -- ∵ f(x)的定义域D=.∴ 数列{xn}只有三项: -- (2)∵ .即 ∴ x=1.或x=2. 即当x0=1或2时. 故当x0=1时.xn=1; 当x0=2时.xn=2 (n∈N). -- 设xn<0 (n∈N). 由 得 得 得 ∵ ∴ 同时使x1.x2.x3为负数的x0不存在. 故所求的x0不存在. --
网址:http://m.1010jiajiao.com/timu3_id_4468029[举报]
定义在(0,+∞)上的函数f(x)满足下列两个条件:(1)对任意的x∈(0,+∞)恒有f(2x)=2f(x)成立;(2)当x∈(1,2]时,f(x)=2-x.如果关于x的方程f(x)=k(x-1)恰有三个不同的解,那么实数k的取值范围是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、-
|
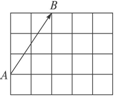
新华网北京10月17日电 北京时间17日2时40分许,记者从北京航天飞控中心获悉,神舟六号飞船返回指令解锁,即将结束五天的太空之旅,踏上返乡路程.凌晨3时43分至48分,远望三号测量船对飞船实施了姿态调整、轨道舱与返回航分离、制动点火等一系列关键控制,仪器表上已准确地出现飞船的方位,飞船顺利进入预定返回轨道.假定把神舟六号飞船看成向量![]() ,现在仪器表屏幕显示在4×5的方格中有一个向量
,现在仪器表屏幕显示在4×5的方格中有一个向量![]() ,以图中的格点为起点和终点作向量,其中与
,以图中的格点为起点和终点作向量,其中与![]() 相等的向量有多少个?与
相等的向量有多少个?与![]() 长度相等的共线向量有多少个?
长度相等的共线向量有多少个?