摘要:记函数的定义域为集合M.函数的定义域为集合.求 (Ⅰ)集合M., (Ⅱ)集合. 如果正三棱锥S-ABC中.底面的边长为3.棱锥的侧面积等于底面积的2倍.M是BC的中点.求 (Ⅰ)的值 (Ⅱ)二面角的大小, (Ⅲ)正三棱锥S-ABC的体积. 已知是等比数列.,是等差数列. (Ⅰ)求数列的通项公式及前项和的公式, (Ⅱ)求数列的通项公式, (Ⅲ)设.其中n=1.2.-.求的值 如图.O为坐标原点.过点且斜率为的直线交抛物线于.两点. (Ⅰ)写出直线的方程, (Ⅱ)求与的值 (Ⅲ)求证: 经过长期观测得到:在交通繁忙的时段内.某公路段汽车的车流量与汽车的平均速度/之间的函数关系为 (Ⅰ)在该时段内.当汽车的平均速度为多少时.车流量最大?最大车流量为多少? (Ⅱ)若要求在该时段内车流量超过10千辆/小时.则汽车的平均速度应在什么范围内? 现有一组互不相同且从小到大排列的数据:其中.为提取反映数据间差异程度的某种指标.今对其进行如下加工:记..作函数.使其图象为逐点依次连接点的折线. (Ⅰ)求和的值, (Ⅱ)设的斜率为.判断的大小关系, (Ⅲ)证明:, (Ⅳ)求由函数y=x与的图象所围成图形的面积(用表示).
网址:http://m.1010jiajiao.com/timu3_id_4467967[举报]
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
.
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数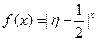 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件 的概率.
的概率.
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
.
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件 的概率.
的概率.
查看习题详情和答案>>
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为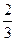 ,被乙小组攻克的概率为
,被乙小组攻克的概率为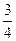 .
.
(1)设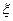 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求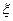 的分布列及
的分布列及 ;
;
(2)设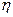 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数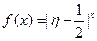 在定义域内单调递增”为事件
在定义域内单调递增”为事件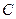 ,求事件
,求事件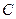 的概率.
的概率.
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为
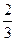 ,被乙小组攻克的概率为
,被乙小组攻克的概率为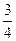 .
.(1)设
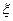 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求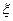 的分布列及
的分布列及 ;
;(2)设
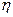 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数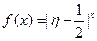 在定义域内单调递增”为事件
在定义域内单调递增”为事件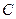 ,求事件
,求事件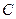 的概率.
的概率. ,考虑到坚固性及用料,要求横断面的面
,考虑到坚固性及用料,要求横断面的面 积为
积为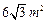 ,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y
,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y m。
m。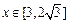 时,横断面用料部分的周长最小?最小值是多少米?
时,横断面用料部分的周长最小?最小值是多少米?
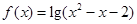 的定义域为集合
的定义域为集合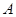 ,函数
,函数 的定义域为集合
的定义域为集合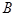 .
.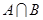 ;
;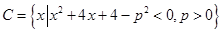 ,且
,且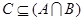 ,求实数
,求实数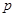 的取值范围.
的取值范围.