摘要：等比数列的公比是负数.则由前项和组成的数列是个( ) A.减数列 B.增数列 C.摆动数列 D.先增后减数列
网址：http://m.1010jiajiao.com/timu3_id_4467702[举报]
已知数列{an}单调递增，且各项非负，对于正整数K，若任意的i，j(1≤i≤j≤K)，aj－ai仍是{an}中的项，则称数列{an}为“K项可减数列”．
(1)已知数列{an}是首项为2，公比为2的等比数列，且数列{bn－2}是“K项可减数列”，试确定K的最大值．
(2)求证：若数列{an}是“K项可减数列”，则其前n项的和
．
(3)已知{an}是各项非负的递增数列，写出⑵的逆命题，判断该逆命题的真假，并说明理由．
已知数列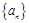
单调递增，且各项非负，对于正整数
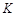，若任意的
，
（
≤≤≤），
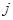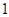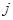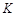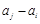仍是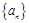中的项，则称数列
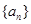为“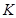
项可减数列”．
（1）已知数列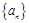是首项为2，公比为2的等比数列，且数列
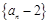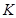是“项可减数
列”，试确定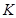的最大值；
（2）求证：若数列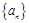是“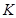项可减数列”，则其前
项的和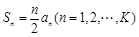
；
（3）已知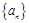是各项非负的递增数列，写出（2）的逆命题，判断该逆命题的真假，
并说明理由．
查看习题详情和答案>>
已知数列
单调递增，且各项非负，对于正整数
，若任意的
，
（
≤≤≤），
仍是中的项，则称数列
为“
项可减数列”．
（1）已知数列是首项为2，公比为2的等比数列，且数列
是“项可减数
列”，试确定的最大值；
（2）求证：若数列是“项可减数列”，则其前
项的和
；
（3）已知是各项非负的递增数列，写出（2）的逆命题，判断该逆命题的真假，
并说明理由．
单调递增，且各项非负，对于正整数，若任意的，（≤≤≤），仍是中的项，则称数列为“项可减数列”．（1）已知数列
是首项为2，公比为2的等比数列，且数列是“项可减数列”，试确定
的最大值；（2）求证：若数列
是“项可减数列”，则其前项的和；（3）已知
是各项非负的递增数列，写出（2）的逆命题，判断该逆命题的真假，并说明理由．