题目内容
已知数列{an}单调递增,且各项非负,对于正整数K,若任意的i,j(1≤i≤j≤K),aj-ai仍是{an}中的项,则称数列{an}为“K项可减数列”.
(1)已知数列{an}是首项为2,公比为2的等比数列,且数列{bn-2}是“K项可减数列”,试确定K的最大值.
(2)求证:若数列{an}是“K项可减数列”,则其前n项的和![]() .
.
(3)已知{an}是各项非负的递增数列,写出⑵的逆命题,判断该逆命题的真假,并说明理由.
答案:
解析:
解析:
|
解:(1)设 (2)因为数列 所以 又由定义知,数列 所以 (3)(2)的逆命题为:已知数列 理由如下:因为 则当 由( 设公差为 |

练习册系列答案
相关题目
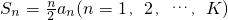 ;
;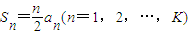 ;
;