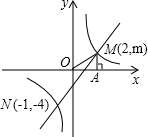
摘要：21．如图.一次函数y=ax+b的图象与反比例函数y=的图象交于M,N两点.M,N两点的坐标分别为M (I)求此反比例函数和一次函数的解析式. 写出使反比例函数值大于一次函数值x的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_446690[举报]
如图，一次函数y=ax+b的图象与x轴，y轴交于A，B两点，与反比例函数y=
的图象相交于C，D两点
，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：
①△CEF与△DEF的面积相等；
②△AOB∽△FOE；
③△DCE≌△CDF；
④AC=BD．
其中正确的结论是 ．（把你认为正确结论的序号都填上）．
查看习题详情和答案>>
| k | x |
，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：①△CEF与△DEF的面积相等；
②△AOB∽△FOE；
③△DCE≌△CDF；
④AC=BD．
其中正确的结论是
如图，一次函数y=ax+b与反比例函数
如图，一次函数y1=ax+b的图象与反比例函数y2=
的图象交于A，B两点，已知OA=
，
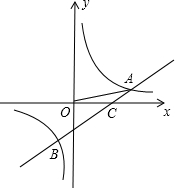tan∠AOC=
，点B的坐标为（-
，m）
（1）求反比例函数的解析式和一次函数的解析式；
（2）观察图象，直接写出使函数值y1＜y2成立的自变量x的取值范围． 查看习题详情和答案>>
| k |
| x |
| 10 |
tan∠AOC=| 1 |
| 3 |
| 3 |
| 2 |
（1）求反比例函数的解析式和一次函数的解析式；
（2）观察图象，直接写出使函数值y1＜y2成立的自变量x的取值范围． 查看习题详情和答案>>
如图，一次函数y=ax+b的图象与反比例函数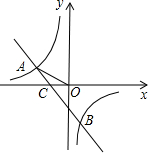
=