摘要：求证(1)1 + cosa =2cos2 ,(2) 1-cosa =2sin2 ,(3) 1 + sina = 2 , (4) 1-sina = 2 ,(5) = tan2. (以上结论可直接当公式使用.主要用来进行代数式的配方化简).
网址：http://m.1010jiajiao.com/timu3_id_4466596[举报]
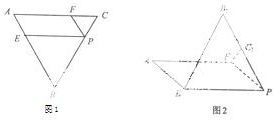如图1，在边长为3的正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足AE=CF=CP=1，今将△BEP、△CFP分别沿EP、FP向上折起，使边BP与边CP所在的直线重合（如图2），B、C折后的对应点分别记为B、C1．（1）求证：PF⊥平面B1EF；
（2）求AB1与平面AEPF所成的角的正弦值． 查看习题详情和答案>>
已知函数f（x）=x3+ax+b+（x∈R），且f（0）=1．
（1）若f（x）在R上单调递增，求实数a的取值范围；
（2）若y=f（x）在x=1处的切线与y轴交于点B，且A（1，f（1）），求d（a）=|AB|2在a∈[c，+∞]的最小值；
（3）若a=-
，Mn=f（1）+
f（2）+
f（3）+…+
f（n）-（1+
+
+…+
），an=
（n∈N*），Sn=a1+a3+…+an，求证：Sn＜
．
查看习题详情和答案>>
（1）若f（x）在R上单调递增，求实数a的取值范围；
（2）若y=f（x）在x=1处的切线与y轴交于点B，且A（1，f（1）），求d（a）=|AB|2在a∈[c，+∞]的最小值；
（3）若a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 2n-1 |
| 6Mn |
| 3 |
| 4 |
在数列{an}中，a1=1，an=
(c为常数，n∈N*，n≥2)．又a1，a2，a5成公比不为1的等比数列．
（Ⅰ）求证{
}为等差数列，并求c的值；
（Ⅱ）设{bn}：b1=
，bn=an-1an+1(n≥2，n∈N*)，Sn为{bn}的前n项和．求
Sn．
查看习题详情和答案>>
| an-1 |
| can-1+1 |
（Ⅰ）求证{
| 1 |
| an |
（Ⅱ）设{bn}：b1=
| 2 |
| 3 |
| lim |
| n→∞ |
A、选修4-1：几何证明选讲