摘要： 如图.正方形ABCD.ABEF的边长都是1.而且平面ABCD.ABEF互相垂直.点M在AC上移动.点N在BF上移动.若CM=BN=a(0<a<). (1)求MN的长, (2)当a为何值时.MN的长最小, (3)当MN长最小时.求面MNA与MNB所成二面角的大小.
网址：http://m.1010jiajiao.com/timu3_id_4466479[举报]
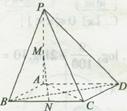
(本小题满分12分)如图，在四棱锥P—ABCD中，底面ABCD是正方形，PA⊥底面ABCD，且PA=AB，M、N分别是PA、BC的中点．
(I)求证：MN∥平面PCD；
(II)在棱PC上是否存在点E，使得AE上平面PBD?若存在，求出AE与平面PBC所成角的正弦值，若不存在，请说明理由
(I)求证：MN∥平面PCD；
(II)在棱PC上是否存在点E，使得AE上平面PBD?若存在，求出AE与平面PBC所成角的正弦值，若不存在，请说明理由
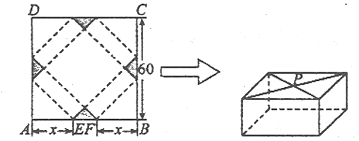
(本小题满分12分)请你设计一个包装盒，如下图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上，是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(cm).
(I)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值？
(II)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值？并求出此时包装盒的高与底面边长的比值.[
查看习题详情和答案>>
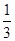CA,用向量法证明：
（1）D、N、M三点共线；（2）若四边形ABCD为正方形，则DN=BN.
图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上，是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(
cm).