摘要:解: (1)从该盒10件产品中任抽4件.有等可能的结果数为种.--------1' 其中次品数不超过1件有种.-------------------2' 被检验认为是合格的概率为-----4'(本步正确.对上两步不作要求) .--------------------6' (2)两次检验是相互独立的.可视为独立重复试验.----------------7' 因两次检验得出该盒产品合格的概率均为. 故“两次检验得出的结果不一致 即两次检验中恰有一次是合格的概率为 -------------10' .----------------11' 答:该盒产品被检验认为是合格的概率为,两次检验得出的结果不一致的概率为. -------------------------------------12' 说明:两小题中没有简要的分析过程.各扣1分. 解:f(x)=cosqsinx-(sinxcosq-cosxsinq)+sinx-sinq =sinqcosx+sinx-sinq.--------------------1¢ 因为f(x)是偶函数. 所以对任意xÎR.都有f(-x)=f(x).--------------------2¢ 即sinqcos(-x)+sin(-x)-sinq=sinqcosx+sinx-sinq, 即sinx=0. 所以tanq=2.-----------------------------5¢ 由-------------------------6¢ 解得 或--------------------------8¢ 此时.f(x)=sinq(cosx-1). 当sinq=时.f(x)=(cosx-1)最大值为0.不合题意最小值为0.舍去,.--9¢ 当sinq=时.f(x)=(cosx-1)最小值为0. 当cosx=-1时.f(x)有最大值为,----------------11¢ 自变量x的集合为{x|x=2kp+p,kÎZ}..-------------------12¢ 解法一: (Ⅰ)建立如图所示的空间直角坐标系. 设. -2¢ 则. --4¢ 于是. ----6¢ . ----7¢ 异面直线与所成的角为. (Ⅱ). . ----10¢ 则. ----11¢ 平面. 又平面. ----12¢ 平面平面. 解法二: (Ⅰ)连结交于点.取中点.连结.则∥. ∴直线与所成的角就是异面直线与所成的角. 设. 则 . . . 中... 直三棱柱中..则. ----4¢ . ----6¢ . ----7¢ 异面直线与所成的角为. (Ⅱ)直三棱柱中..平面. ----8¢ 则. 又... ----10¢ 则. 于是. 平面. 又平面. 平面平面. 解:(I)设f(x)=ax2+bx+c.则f ¢(x)=2ax+b.------------------1¢ 由题设可得:即----------------4¢ 解得----------------------------5¢ 所以f(x)=x2-2x-3.--------------------------6¢ (II)g(x)=f(x2)=x4-2x2-3.g ¢(x)=4x3-4x=4x(x-1)(x+1).---------8¢ 列表: x -1 0 (0,1) 1 f¢(x) - 0 + 0 - 0 + f(x) ↘ ↗ ↘ ↗ ---------------------------------11¢ 由表可得:函数g(x)的单调递增区间为.---------12¢ 解:(Ⅰ)时.的项都是中的项,-------2' 时.的项不都是中的项.--------3' (Ⅱ)时.-------------------4' -----------------------5' 的项一定都是中的项.-----------------------------7' (Ⅲ)当且仅当取时.的项都是中的项.理由是:-----------------------------------9' ①当时. 时.. 其中是的非负整数倍.设为(). 只要取即(为正整数)即可得.即的项都是中的项,--11' ②当时.不是整数.也不可能是的项.----12' 解:(Ⅰ)①若直线∥轴.则点为,------------------1' ②设直线.并设点的坐标分别是. 由消去.得 . ①--------2' 由直线与椭圆有两个不同的交点.可得.即.所以.-----------------------4' 由及方程①.得. . 即----------------------------6' 由于(否则.直线与椭圆无公共点).将上方程组两式相除得..代入到方程.得.整理.得(. 综上所述.点的轨迹方程为(.--------8' (Ⅱ)①当∥轴时.分别是椭圆长轴的两个端点.则点在原点处.所以..所以.,-----------------9' ②由方程①.得 所以.. . 所以.-------------------12' 因为.所以.所以.所以. 综上所述..----------------------14'
网址:http://m.1010jiajiao.com/timu3_id_4466262[举报]
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当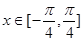 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
查看习题详情和答案>>
((本小题满分12分)
编号分别为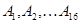 的16名篮球运动员在某次比赛中得分记录如下;
的16名篮球运动员在某次比赛中得分记录如下;
|
编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
|
得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
|
编号 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
|
得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间的人数填入相应的空格内:
|
区 间 |
|
|
|
|
人 数 |
|
|
|
(Ⅱ)从得分在区间 内的运动员中随机抽取2人.
内的运动员中随机抽取2人.
(1)用运动员编号列出所有可能的抽取结果;
(2)求这两人得分之和大于50的概率.
查看习题详情和答案>>
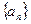 中,
中,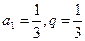 ,
,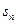 为数列
为数列 项的和,证明:
项的和,证明:
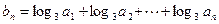 ,求数列
,求数列 的通项公式;
的通项公式;