摘要：如图.E.F.M.N是正方体的四个顶点.记d1为F到面FMN的距离.d2为E面EMN的距离.d3为M到面EFN的距离.那么d1,d2,d3的大小关系为 A．d1＜d2＜d3 B．d2＜d3＜d1 C．d2＜d1＜d3 D．d3＜d2＜d1 联想:(1)三棱柱ABC-A1B1C1的体积为V.P.Q分别为AA1.CC1上的点.而且满足PA=QC1.则VB-APQC= A. B. C. D. (2)如图.多面体ABCDFE中.ABCD是边长为3的正方形.EF∥平面ABCD.EF=.EF到面ABCD的距离为2.则多面体的体积为 A． B．5 C．6 D．
网址：http://m.1010jiajiao.com/timu3_id_4466034[举报]
6、如图，在正方体ABCD-A1B1C1D1中，E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点，N是BC的中点，点M在四边形EFGH上及其内部运动，则M满足条件
M∈FH
时，有MN∥平面B1BDD1．
8、如图，已知正方体ABCD-A1B1C1D1的棱长为3，点E，F在线段AB上，点M在线段B1C1上，点N在线段C1D1上，且EF=1，D1N=x，AE=y，M是B1C1的中点，则四面体MNEF的体积（ ）
查看习题详情和答案>>
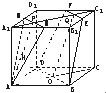如图，在正方体ABCD-A1B1C1D1中，M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点，AB=a．（1）求证：平面AMN∥平面EFDB；
（2）求异面直线BE与MN之间的距离． 查看习题详情和答案>>
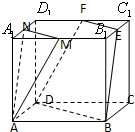如图，正方体ABCD-A1B1C1D1中，M，N，E，F分别是棱A1B1，A1D1，B1C1，C1D1的中点．
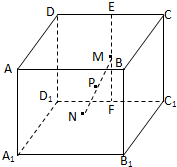如图，正方体ABCD-A1B1C1D1的棱长为4，E，F分别是棱CD、C1D1的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A1B1C1D1上运动，则线段MN的中点P的轨迹（曲面）与二面角D-C1D1-B1所围成的几何体的体积为