摘要： P是以F1.F2为焦点的双曲线上的一点.PF1⊥PF2.且则双曲线的离心率e= .
网址：http://m.1010jiajiao.com/timu3_id_4465617[举报]
P是以F1、F2为焦点的双曲线C：
-
=1（a＞0，b＞0）上的一点，已知
•
=0，|
|=2|
|．
（1）试求双曲线的离心率e；
（2）过点P作直线分别与双曲线两渐近线相交于P1、P2两点，当
•
=-
，2
+
=0，求双曲线的方程．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
（1）试求双曲线的离心率e；
（2）过点P作直线分别与双曲线两渐近线相交于P1、P2两点，当
| OP1 |
| OP2 |
| 27 |
| 4 |
| PP1 |
| PP2 |
上的一点，若
，tan∠PF
B.5 C.2
D.3P是以F1、F2为焦点的双曲线C：
-
=1（a＞0，b＞0）上的一点，已知
•
=0，|
|=2|
|．
（1）试求双曲线的离心率e；
（2）过点P作直线分别与双曲线两渐近线相交于P1、P2两点，当
•
=-
，2
+
=0，求双曲线的方程．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
（1）试求双曲线的离心率e；
（2）过点P作直线分别与双曲线两渐近线相交于P1、P2两点，当
| OP1 |
| OP2 |
| 27 |
| 4 |
| PP1 |
| PP2 |
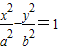（a＞0，b＞0）上的一点，已知
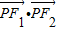=0，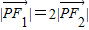
．
=-
，
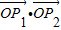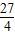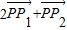=0，求双曲线的方程．
上的一点，若
，
，则此双曲线的离心率为
B．3 C．5 D．