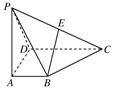
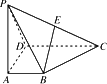
摘要:16.如图.四棱锥P-ABCD的底面为一直角梯形.BA⊥AD.CD⊥AD.CD=2AB.PA⊥底面ABCD.E为PC中点.(1)证明:平面PDC⊥平面PAD, (2)证明:EB∥平面PAD,(3)若PA=AD.证明:BE⊥平面PDC. 答案:BAAA DBCC 9. 10.16或64 11. 12.②③ 13. 14.①②③ 15.(2) 16.(略)
网址:http://m.1010jiajiao.com/timu3_id_4465217[举报]
如图,四棱锥P-ABCD的底面为一直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点.
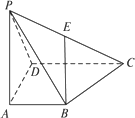
(1)证明EB∥平面PAD.
(2)若PA=AD,证明BE⊥平面PDC.
如图,四棱锥P-ABCD的底面为菱形,且∠ABC-120°,PA⊥底面ABCD,AB=1,PA=![]() ,E为PC的中点.
,E为PC的中点.
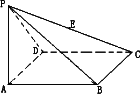
(1)求直线DE与平面PAC所成角的大小;
(2)求二面角E―AD―C的平面角的正切值;
(3)在线段PC上是否存在一点M,使PC⊥平面MBD成立?如果存在,求出MC的长;如果不存在,请说明理由.