题目内容
 本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
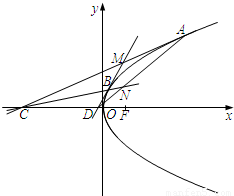
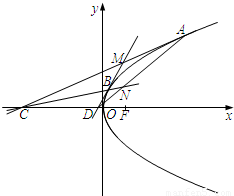
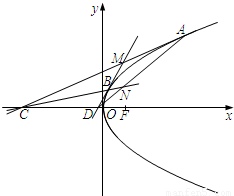
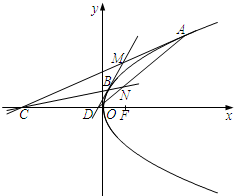
如图,在平面直角坐标系xOy,抛物线的顶点在原点,焦点为F(1,0).过抛物线在x轴上方的不同两点A、B,作抛物线的切线AC、BD,与x轴分别交于C、D两点,且AC与BD交于点M,直线AD与直线BC交于点N.
(1)求抛物线的标准方程;
(2)求证:MN⊥x轴;
(3)若直线MN与x轴的交点恰为F(1,0),求证:直线AB过定点.
(1)解:由题意,可设抛物线的标准方程为y2=2px(p>0),则 ,即p=2.
,即p=2.
所以抛物线的标准方程为y2=4x.…(3分)
(2)证明:设A(x1,y1),B(x2,y2),且y1>0,y2>0.
由y2=4x(y>0),得y=2 ,所以y′=
,所以y′= .
.
所以切线AC的方程为y-y1=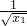 (x-x1),即y-y1=
(x-x1),即y-y1=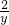 (x-x1).
(x-x1).
整理,得yy1=2(x+x1),①且C点坐标为(-x1,0).
同理得切线BD的方程为yy2=2(x+x2),②且D点坐标为(-x2,0).
由①②消去y,得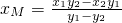 .
.
又直线AD的方程为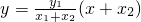 ,③
,③
直线BC的方程为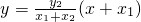 . ④
. ④
由③④消去y,得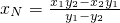 .
.
所以xM=xN,即MN⊥x轴.
(3)证明:由题意,设M(1,y0),代入(1)中的①②,得y0y1=2(1+x1),y0y2=2(1+x2).
所以A(x1,y1),B(x2,y2)都满足方程y0y=2(1+x).
所以直线AB的方程为y0y=2(1+x).
故直线AB过定点(-1,0).
分析:(1)设抛物线的标准方程为y2=2px(p>0),利用焦点为F(1,0),可求抛物线的标准方程;
(2)设A(x1,y1),B(x2,y2),求出切线AC、BD的方程,求得M的横坐标,求出直线AD、BC的方程,求得N的横坐标,即可证得结论;
(3)求得A(x1,y1),B(x2,y2)都满足方程y0y=2(1+x),即直线AB的方程为y0y=2(1+x),从而可得结论.
点评:本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力
 ,即p=2.
,即p=2.所以抛物线的标准方程为y2=4x.…(3分)
(2)证明:设A(x1,y1),B(x2,y2),且y1>0,y2>0.
由y2=4x(y>0),得y=2
 ,所以y′=
,所以y′= .
.所以切线AC的方程为y-y1=
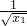 (x-x1),即y-y1=
(x-x1),即y-y1=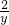 (x-x1).
(x-x1).整理,得yy1=2(x+x1),①且C点坐标为(-x1,0).
同理得切线BD的方程为yy2=2(x+x2),②且D点坐标为(-x2,0).
由①②消去y,得
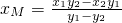 .
.又直线AD的方程为
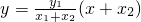 ,③
,③直线BC的方程为
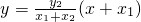 . ④
. ④由③④消去y,得
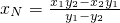 .
.所以xM=xN,即MN⊥x轴.
(3)证明:由题意,设M(1,y0),代入(1)中的①②,得y0y1=2(1+x1),y0y2=2(1+x2).
所以A(x1,y1),B(x2,y2)都满足方程y0y=2(1+x).
所以直线AB的方程为y0y=2(1+x).
故直线AB过定点(-1,0).
分析:(1)设抛物线的标准方程为y2=2px(p>0),利用焦点为F(1,0),可求抛物线的标准方程;
(2)设A(x1,y1),B(x2,y2),求出切线AC、BD的方程,求得M的横坐标,求出直线AD、BC的方程,求得N的横坐标,即可证得结论;
(3)求得A(x1,y1),B(x2,y2)都满足方程y0y=2(1+x),即直线AB的方程为y0y=2(1+x),从而可得结论.
点评:本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
(2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.