摘要:使得Cn1+Cn2+Cn2+-Cnn<2003不成立的最小的正整数n的值为 A.8 B.9 C.10 D.11
网址:http://m.1010jiajiao.com/timu3_id_4464868[举报]
已知数列{an}的通项公式为an=2n-1+1.
(1)若Sn=a1Cn0+a2Cn1+a3Cn2+…+an+1Cnn,(n∈N*),求证:当n为偶数时,Sn-2n-4n-1能被64整除.
(2)是不是存在等差数列{bn},使得b1Cn1+b2Cn2+…+bnCnn=n(an-1)对一切n∈N*都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由.
(3)记Tn=1!Cn1+2!Cn2+3!Cn3+…+n!Cnn(n=1,2,3,…),当n≥2时,求证:(1+
)(1+
)(1+
)…(1+
)≤3-
.
查看习题详情和答案>>
(1)若Sn=a1Cn0+a2Cn1+a3Cn2+…+an+1Cnn,(n∈N*),求证:当n为偶数时,Sn-2n-4n-1能被64整除.
(2)是不是存在等差数列{bn},使得b1Cn1+b2Cn2+…+bnCnn=n(an-1)对一切n∈N*都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由.
(3)记Tn=1!Cn1+2!Cn2+3!Cn3+…+n!Cnn(n=1,2,3,…),当n≥2时,求证:(1+
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| T3 |
| 1 |
| Tn |
| 1 |
| 1+log2(an-1) |
 )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )≤3-
)≤3- .
.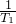 )(1+
)(1+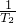 )(1+
)(1+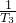 )…(1+
)…(1+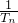 )≤3-
)≤3-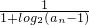 .
.