摘要：19．(1)若CD平面PAD.则CDPD.由已知PC=PD.得PCD=PDC<90°.这与CDPD矛盾.所以CD与平面QAD不垂直. (2)取AB.CD的中点E.F.联结PE.PF.EF.由PA=PB.PC=PD.得PEAB.PFCD.EF为直角梯形的中位线.EFCD.又PFEF=F.CD平面PEF.由PE平面PEF.得CDPE.又ABPE且梯形两腰AB.CD必相交.PE平面ABCD.又PE墙面PAB.平面PAB平面ABCD. - 及二面角定义可知PFE为二面角P-CD-A的平面角.做EGBC于G.连PG.由三垂线定理得BCPG.故PGE为二面角P-CD-A的平面角.即PGE=60°.由已知.得EF==CD.又EG=CF=CD.EF=EG.易证得RtPEF = RtPEG.PFE=PGE=60°.即为所求.
网址：http://m.1010jiajiao.com/timu3_id_4463645[举报]
（本小题满分12分）
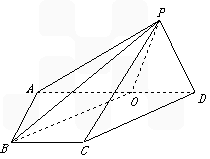
如图，在四棱锥P－ABCD中，侧面PAD⊥底面ABCD，侧棱PA⊥PD，底面ABCD是直角梯形，其中BC∥AD，∠BAD＝90°，AD＝3BC，O是AD上一点．
(1)若CD∥平面PBO，试指出点O的位置，并说明理由；
(2)求证：平面PAB⊥平面PCD.
查看习题详情和答案>>
如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD，侧棱PA⊥PD，底面ABCD为直角梯形．其中BC∥AD，∠BAD=90°，AD=3BC，O是AD上一点①若CD∥平面PBO 试指出O的位置并说明理由
②求证平面PAB⊥平面PCD
③若PD=BC=1，AB=2
| 2 |
如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD，侧棱PA⊥PD，底面ABCD为直角梯形．其中BC∥AD，∠BAD=90°，AD=3BC，O是AD上一点
①若CD∥平面PBO 试指出O的位置并说明理由
②求证平面PAB⊥平面PCD
③若PD=BC=1，AB=
，求P-ABCD的体积．
查看习题详情和答案>>
①若CD∥平面PBO 试指出O的位置并说明理由
②求证平面PAB⊥平面PCD
③若PD=BC=1，AB=
，求P-ABCD的体积．
查看习题详情和答案>>
