摘要：20．如图.设定直线L1:x=-,定点F(.0).其中＞0.动直线L2垂直L1与点P.线 段PF的垂直平分线交L2与点M. (1)求点M的轨迹C的方程. (2)设点M的轨迹C与x轴交于点Q.在C上是否一定存在另外两点R.S.使得ΔQRS 为等边三角形?若存在.请用表示这个等边三角形的面积,若不存在.请说明理由. 解: 高三第二学期导师制(04)解答
网址：http://m.1010jiajiao.com/timu3_id_4463247[举报]
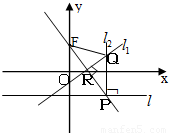
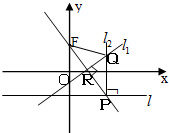
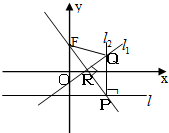如图，在平面直角坐标系xoy中，设点F（0，p）（p＞0），直线l：y=-p，点p在直线l上移动，R是线段PF与x轴的交点，过R、P分别作直线l1、l2，使l1⊥PF，l2⊥l l1∩l2=Q．
（Ⅰ）求动点Q的轨迹C的方程；
（Ⅱ）在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
（Ⅲ）对（Ⅱ）求证：当直线MA，MF，MB的斜率存在时，直线MA，MF，MB的斜率的倒数成等差数列．
查看习题详情和答案>>
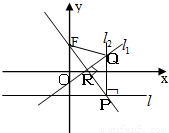
如图，在平面直角坐标系xoy中，设点F(0,p)（p＞0），直线l:y=-p，点P在直线l上移动，R是线段PF与x轴的交点, 过R、P分别作直线l1、l2，使l1⊥PF，l2⊥l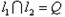 
．
（Ⅰ）求动点Q的轨迹C的方程；
（Ⅱ）在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
（Ⅲ）对（Ⅱ）求证：当直线MA,MF,MB的斜率存在时，直线MA,MF,MB的斜率的倒数成等差数列．
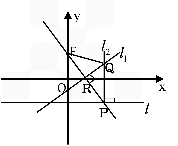
如图，在平面直角坐标系xoy中，设点F（0，p）（p＞0），直线l：y=-p，点p在直线l上移动，R是线段PF与x轴的交点，过R、P分别作直线l1、l2，使l1⊥PF，l2⊥l l1∩l2=Q．
（Ⅰ）求动点Q的轨迹C的方程；
（Ⅱ）在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
（Ⅲ）对（Ⅱ）求证：当直线MA，MF，MB的斜率存在时，直线MA，MF，MB的斜率的倒数成等差数列．
查看习题详情和答案>>
（Ⅰ）求动点Q的轨迹C的方程；
（Ⅱ）在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
（Ⅲ）对（Ⅱ）求证：当直线MA，MF，MB的斜率存在时，直线MA，MF，MB的斜率的倒数成等差数列．
查看习题详情和答案>>
