摘要:设集合S n=.若X是Sn的子集.把X的所有数的乘积称为X的容量(若X中只有一个元素.则该元素的数值即为它的容量.规定空集的容量为0).若X的容量为奇(偶)数.则称X为Sn的奇(偶)子集.若n=4.则Sn的所有奇子集的容量之和为 .
网址:http://m.1010jiajiao.com/timu3_id_4463136[举报]
设集合S?N*,S≠∅,且满足(1)1∉S;(2)若x∈S,则1+
∈S.
(1)S能否为单元集,为什么?
(2)求出只含两个元素的集合S.
(3)满足题设条件的集合S共有几个?为什么?能否列举出来. 查看习题详情和答案>>
| 12 | x-1 |
(1)S能否为单元集,为什么?
(2)求出只含两个元素的集合S.
(3)满足题设条件的集合S共有几个?为什么?能否列举出来. 查看习题详情和答案>>
设集合S?N*,S≠∅,且满足(1)1∉S;(2)若x∈S,则1+
∈S.
(1)S能否为单元集,为什么?
(2)求出只含两个元素的集合S.
(3)满足题设条件的集合S共有几个?为什么?能否列举出来.
查看习题详情和答案>>
| 12 |
| x-1 |
(1)S能否为单元集,为什么?
(2)求出只含两个元素的集合S.
(3)满足题设条件的集合S共有几个?为什么?能否列举出来.
设集合S?N*,S≠∅,且满足(1)1∉S;(2)若x∈S,则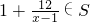 .
.
(1)S能否为单元集,为什么?
(2)求出只含两个元素的集合S.
(3)满足题设条件的集合S共有几个?为什么?能否列举出来.
查看习题详情和答案>>
(2013•泸州一模)设集合s为非空实数集,若数η(ξ)满足:
(1)对?x∈S,有x≤η(x≥ξ),即η(ξ)是S的上界(下界);
(2)对?a<η(a>ξ),?xo∈S,使得xo>a(xo<a),即η(ξ)是S的最小(最大)上界(下界),则称数η(ξ)为数集S的上(下)确界,记作η=supS(ξ=infS).
给出如下命题:
①若 S={x|x2<2},则 supS=-
;
②若S={x|x=n|,x∈N},则infS=l;
③若A、B皆为非空有界数集,定义数集A+B={z|z=x+y,x∈A,y∈B},则sup(A+B)=supA+supB.
其中正确的命题的序号为
查看习题详情和答案>>
(1)对?x∈S,有x≤η(x≥ξ),即η(ξ)是S的上界(下界);
(2)对?a<η(a>ξ),?xo∈S,使得xo>a(xo<a),即η(ξ)是S的最小(最大)上界(下界),则称数η(ξ)为数集S的上(下)确界,记作η=supS(ξ=infS).
给出如下命题:
①若 S={x|x2<2},则 supS=-
| 2 |
②若S={x|x=n|,x∈N},则infS=l;
③若A、B皆为非空有界数集,定义数集A+B={z|z=x+y,x∈A,y∈B},则sup(A+B)=supA+supB.
其中正确的命题的序号为
③
③
(填上所有正确命题的序号). ;
;