题目内容
设集合s为非空实数集,若数η(ξ)满足:
(1)对?x∈S,有x≤η(x≥ξ),即η(ξ)是S的上界(下界);
(2)对?a<η(a>ξ),?xo∈S,使得xo>a(xo<a),即η(ξ)是S的最小(最大)上界(下界),则称数η(ξ)为数集S的上(下)确界,记作η=supS(ξ=infS).
给出如下命题:
①若 S={x|x2<2},则 supS=- ;
;
②若S={x|x=n|,x∈N},则infS=l;
③若A、B皆为非空有界数集,定义数集A+B={z|z=x+y,x∈A,y∈B},则sup(A+B)=supA+supB.
其中正确的命题的序号为________(填上所有正确命题的序号).
解:①由x2<2,得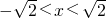 ,∴
,∴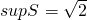 ,故①不正确;
,故①不正确;
②∵x∈N,∴infS=0,故②不正确;
③∵?x∈A,?y∈B,∴x≤supA,y≤supB,
∴z=x+y≤supA+supB,
∴sup(A+B)≤supA+supB;
同理supA+supB≤sup(A+B);
故sup(A+B)=supA+supB.
故③正确.
故答案为③.
分析:①由上确界的定义可得supS= ;
;
②由下确界的定义可得infS=0;
③利用上下确界的定义即可证明正确.
点评:正确理解新定义是解题的关键.
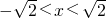 ,∴
,∴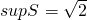 ,故①不正确;
,故①不正确;②∵x∈N,∴infS=0,故②不正确;
③∵?x∈A,?y∈B,∴x≤supA,y≤supB,
∴z=x+y≤supA+supB,
∴sup(A+B)≤supA+supB;
同理supA+supB≤sup(A+B);
故sup(A+B)=supA+supB.
故③正确.
故答案为③.
分析:①由上确界的定义可得supS=
 ;
;②由下确界的定义可得infS=0;
③利用上下确界的定义即可证明正确.
点评:正确理解新定义是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 ;
; ;
;